Loading... ## 上一周的学习内容 ### 1. 神经网络 #### 1.1 神经元模型 神经网络中最基本的成分为神经元模型. 常用的模型为 `M-P神经模型`, 神经元收到 $n$ 个其他神经元传递过来的信号, 通过带权重的连接进行传递. 再将接收到的总输入值与神经元阈值进行比较, 通过 `激活函数(Activation Function)` 处理神经元的输出. 即线性组合通过非线性的模式表示出来, $$ y = f(\sum^n_{i=1} w_i x_i - \theta) $$ #### 1.2 感知机与多层网络 ##### 感知机 `感知机(Perceptron)`: 由两层神经元组成, 输入层接受输入信号给输出层, 输出层为M-P神经元 > `感知机` 在输入层未做神经元变换, 在输出层做非线性变换 对于感知机的学习规则: 对于训练样例 $(x, \hat{y})$, 当前的输出为 $y$, 则权重调整规则为: $$ w_i \leftarrow w_i + \Delta w_i $$ $$ \Delta w_i = \eta (\hat{y} - y) x_i $$ > - 规则类似于梯度下降 > - $\eta \in (0,1)$ 为学习率 > - 当 $y=\hat{y}$ 时, 感知机不发生变化, 此时称为 `收敛(converge)` 因为感知机只有 $1$ 层功能神经元, 所以学习能力有限. 若两类模式 `线性可分(linearly separable)`, 则感知机学习过程一定会 `收敛(converge)`; 反之会发生 `震荡(fluctuation)` > - `线性可分(linearly separable)`: 可以用一条直线将超平面分割, 将所有值划分两类, 成为线性可分 > - 解决线性不可分问题通常需要考虑多层功能神经元(即包含`隐藏层(hidden layer)`) ##### 多层神经网络 更常见的神经网络一般为层级结构. `多层前馈神经网络(multi-layer feedforward neural networks)`: 每层神经元与下一层互相全连接, 也不存在跨层连接. 输入层神经元接受外界输入, 隐藏层和输出层神经元对信号进行加工. 学习过程: 根据训练数据调整神经元之间的`连接权(connection weight)`, 以及每个功能神经元的阈值. #### 1.3 误差逆传播算法 又称`反向传播算法`, 简称 `BP算法 `. 是一个迭代学习算法, 在迭代的每一轮中采用广义的感知机学习规则对参数进行更新估计. 目的是最小化训练集 $D$ 的累计误差 $E=\frac{1}{m}\sum^{m}_{k=1}E_k$ ##### 算法过程 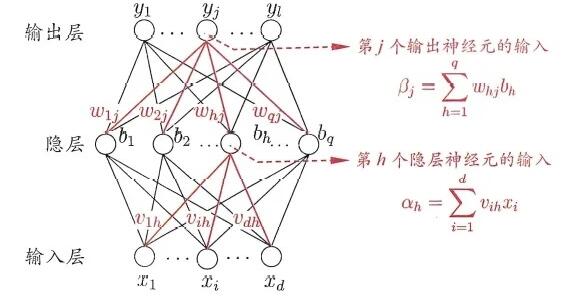 定义: - $\theta_j$: 输出层第 $j$ 个神经元的阈值 - $\gamma_h$: 隐层第 $h$ 个神经元的阈值 - 其余定义见图 对训练例 $(x_k, y_k)$, 假定输出为 $y_k=(y^k_1,y^k_2,\ldots,y^k_l)$, 即 $$ y_j=f(\beta_j, \theta_j) $$ , 定义Loss函数 $$ E_k=\frac{1}{2}\sum^{l}_{j=1}(y_j^k-\hat{y_j^k})^2 $$ > $\frac{1}{2}$ 仅为方便计算 每一轮采用广义的感知机学习规则对参数进行更新, 对于任意参数 $v$: $$ v \leftarrow v + \Delta v $$ > - $v$ 有初始值, 通过梯度下降进行修正 > - 在网络中一共有 $(d+l+1)q+l$ 个参数需要确定, 其中 > - 输入层到隐层: $q \times l$ > - 隐层神经元阈值: $q$ > - 输出层层神经元阈值: $l$ --- ###### $\Delta w_{hj}$ 为例 基于梯度下降策略, 对参数进行调整 $$ \Delta w_{hj} = -\eta \frac{\partial E_k}{\partial w_{hj}} $$ $$ \frac{\partial E_k}{\partial w_{hj}} = \frac{\partial E_k}{\partial y_j^k} \cdot \frac{\partial y_j^k}{\partial \beta_j} \cdot \frac{\partial \beta_j}{\partial w_{hj}} $$ > 使用链式法则进行微分, 其中 > > - $\frac{\partial E_k}{\partial y_j^k}$: 先对输出层求导 > - $\frac{\partial y_j^k}{\partial \beta_j}$: 对输出层的输入求导(即对`sigmoid`函数进行求导) > - $\frac{\partial \beta_j}{\partial w_{hj}}$: 输出层的输入对参数值求导 根据 $\beta_j$ 定义得到 $$ \frac{\partial \beta_j}{\partial w_{hj}} = b_h $$ > 是线性的 令 $$ \begin{aligned} g_i &= -\frac{\partial E_k}{\partial y_j^k} \cdot \frac{\partial y_j^k}{\partial \beta_j} \\ &=y^k_j(1-y^k_j)(\hat{y^k_j}-y^k_j) \end{aligned} $$ > 根据sigmoid函数求导, $f'(x)=f(x)(1-f(x))$ 根据上面的两个式子得到 $$ \Delta w_{hj} = \eta g_j b_h $$ --- 类似得到 $$ \Delta \theta_{j} = -\eta g_j $$ $$ \Delta v_{ih} = -\eta e_h x_i $$ $$ \Delta \gamma_h = -\eta e_h $$ --- > 以上过程称之为 `标准BP算法` ##### 累积BP算法 `累积误差逆传播算法 (accumulated error backpropagation)`, 特点: - 同标准BP算法类似, 但并不基于累积误差最小化的更新规则, 而是即遍历后再更新参数 - 是直接针对训练集的累计误差最小化优化 - 累积误差下降到一定程度后,进一步下降会非常缓慢 #### 1.4 局部最小和全局最小 > Ref: 李宏毅机器学习Ch2的笔记 #### 1.5 常见的神经网络 ##### RBF网络 是一种单隐层前馈神经网络, 它使用径向基函数作为隐层神经元激活函数, 而输出层是对隐层神经元输出的线性组合. 对激活函数进行了改进. ##### ART网络 一种基于`竞争性学习`的网络. 可以在训练过程中动态增长以增加新的模式类. 优点在于可以进行`在线学习(online learning)` > `竞争性学习(competitive learning)`: 常用的无监督学习策略, 输出元相互竞争, 每一时刻只有一个神经元被激活,其余则被抑制. ##### SOM网络 即 `自组织映射网络(Self-Organizing Map)`, 是一种竞争学习型的无监督神经网络, 它能将高维输入数据映射到低维空间,同时保持输入数据在高维空间的拓扑结构. ##### 级联相关网络 ##### Elman网络 `循环神经网络`, 允许网络中出现环形结构,从而可让一些神经元的输出反馈回来作为输入信号. 特点是将上一层的输出作为该层的输入. 隐层神经元通常采用Sigmoid函数 ##### Boltzmann机 是一种`基于能量的模型(energy-based model)`, 为网络状态定义一个`能量(energy)`, 能量最小化时网络达到理想状态, 网络的训练就是在最小化这个能量函数 特点: Boltzmann机中的神经元都是布尔型的, 即只能取01两种状态,状态1表示激活, 状态0表示抑制. #### 1.6 深度学习 - 理论上来说, 参数越多的模型复杂度越高, 容量越大,这意味着它能完成更复杂的学习任务 - 一般情形下, 复杂模型的训练效率低, 易陷入过拟合 - 计算能力的大幅提高可缓解训练低效性, 训练数据的大幅增加则可降低过拟合风险 ##### 产生的问题 使用经典算法进行训练时, 因为误差在多隐层内逆传播时, 往往会发散而不嗯呢该收敛达到稳定状态 ##### 解决方法 - 无监督逐层训练(unsupervised layer-wise training), 预训练-调优(Pre-training/Fine-turning) - 权共享(weight sharing) --- ### 2. CNN & Self-attention #### 2.1 CNN ##### 图像的表达形式 一张输入的图像其实是一个三维的张量, **三个维度分别表示图像的宽, 高和Channel数目**, 彩色图像的每一个像素都是由RGB三个颜色所组成的, 所以3个Channel就分别代表了RGB三个颜色,宽和高表示了这张图像中像素的数目. 将这个三维的张量拉直成一个向量, 每一维里存的数值表示某一个像素在某个颜色上的强度. 使用 `Fully Connected Network` 来实现目标, **随着网络层数增多, 参数也增多, 网络的弹性增强, 更容易出现过拟合问题, 训练的效率也会变低**. 因此 `Fully Collected Network` 并不适合直接拿来处理图像信息, 需要做进一步的简化. ##### 识别图像的特征(Pattern) 用于图像分类的类神经网络是通过综合检测到的一些重要的 patterns 来进行分类, 因此没必要将一整张图像的每个神经元的输入. 只需要将一小部分输入到神经元就可以检测到某些重要的patterns. ##### 解决方法: 感受野 (Receptive Field) 一般在CNN中设置有感受野, 并由一组神经元来处理这个感受野提取的图像信息. 一般感受野是要考虑所有Channels上的信息的. > 在描述感受野时, 只要说明宽和高(Kernel Size). 选取感受野: 1. 感受野可以有大有小 2. 可以指考虑一个Channel (对于CNN模型并不常用) 3. 感受野可以为长方形 通常的设置: 1. 通常考虑所有的 Channel (kernal size: 3x3) 2. 移动的值`Stride`通常设为1或2 3. 超出的范围做`Padding`处理(一般为补0) 4. 图像的每一个位置都应被`neural`照顾到 ##### 图像的Pattern出现在不同位置的处理方式 解决方法: 共享参数. 例如存在两个`neural`, 1. **neural 1**: $\sigma(w_1 x_1 + w_2 x_2 + \cdots)$ 2. **neural 2**: $\sigma(w_1 x_1' + w_2 x_2' + \cdots)$ 都采用相同的 $(w_1, w_2, \cdots)$ 通常的设置: - 每个感受野有一组`neural`照顾到 - 公用的参数称之为Filter[1,2,3,...] 因此, 相较于`全连接网络`, `感受野` 和 `参数共享` 限制了网络的弹性. `感受野` 和 `参数共享` 组成了 `Convolution Layer`, 拥有较大的 `Model bias` #### 2.2 Self-attention (自注意力机制) 输入可以是一个向量, 也可以是一组向量. 例如 - 处理一段文字时, 每个单词作为一组向量. 通常有 `One-hot encoding` 和 `Word embadding` 两种方法处理文字 - 处理一段音频时, 将一段音频分为若干个帧, 一个帧作为一组向量. - 处理一个图(Graph)时, 一个Node作为一个向量 通常多向量输入的模型输出分为三种情况: - 每个向量对应一个输出Label - 只输出1个Label - 自己决定输出多少个Label (Seq2Seq, 如翻译) ##### 对于每个向量对应一个输出Label 假设存在 $a = (a_1, a_2, a_3, a_4)$ 四个输入, 采用`Self-attention`的步骤如下 1. 计算$a_i$, $a_j$的关联程度 - `dot-product`: $q = a^i W^q$, $k = a^j W^k$, $\alpha = q \cdot k$ - 通常对 $\alpha$ 做 `soft-max`, 得到 $\alpha '$ 2. 根据 $\alpha '$ 抽取特征 - $v^i=W^v a^i$ - $b^1=\sum\alpha'_{1,i}v^i$ > - $\alpha$ 称为 `attention score` > - $q$ 称为 `query` > - $k$ 称为 `key` ##### 矩阵方式表达 令 $Q = (q_1, q_2, q_3, q_4)$, $I = (a_1, a_2, a_3, a_4)$, $V = (v_1, v_2, v_3, v_4)$, $O = (b_1, b_2, b_3, b_4)$ $$ Q = W^q I $$ $$ K = W^k I $$ $$ V = W^v I $$ $$ A = \begin{bmatrix} \alpha_{1,1} & \cdots & \alpha_{1,4} \\ \vdots & & \vdots \\ \alpha_{4,1} & \cdots & \alpha_{4,4} \end{bmatrix}= k^T Q \rightarrow^{softmax} A' $$ $$ O = (v_1, v_2, v_3, v_4) \begin{bmatrix} \alpha_{1,1} & \cdots & \alpha_{1,4} \\ \vdots & & \vdots \\ \alpha_{4,1} & \cdots & \alpha_{4,4} \end{bmatrix}= VA' $$ 因此, $W^q, W^k, w^v$ 为需要被学习的参数 ##### Position Embedding 如果输入的各个向量对位置有所要求, 通常做 `Position Embedding` 1. 为每一个不同位置设置向量: $e^i$ 2. $a^i \leftarrow e^i+a^i$ ## 本周学习计划 1. 完成Ch.5 神经网络的一些公式和习题 2. 周志华 《机器学习》 Ch.6 支持向量机 3. 李宏毅2021春机器学习课程 Ch.5 Transformer 4. 看2篇论文 最后修改:2021 年 07 月 26 日 © 允许规范转载 赞 0 如果觉得我的文章对你有用,请随意赞赏