Loading... ## 上一周的学习内容 ### 1. 决策树 `决策树 (decision tree)` 是一类常见的机器学习方法. 是基于树结构来进行决策的. ``` A=? (A=1) / \ (...) / \ B=? ... (B=1) / \ (...) / \ C=? ... (C=1) / \ (...) / \ D ... ``` 中间结点是决策过程, 叶结点是决策结果, 根节点包含样本全集. `决策树` 的学习算法是一个 **递归算法**.  #### 决策树划分选择 决策树学习的关键在于如何选择划分属性, 不同的划分属性得出不同的分支结构, 从而影响整颗决策树的性能. 属性划分的目标是让各个划分出来的子节点尽可能地属于同一类别. 决策树最常用的算法有三种: `ID3`, `C4.5`, `CART`. ##### 1. ID3算法 `ID3` 算法使用 **信息增益为准则** 来选择划分属性, `信息熵(information entropy)` 是度量样本结合纯度的常用指标. 假定当前样本集合 $D$ 中第 $k$ 类样本所占比例为$p_k$,则样本集合 $D$ 的信息熵定义为 $$ \text{Ent}(D) = -\sum^{|D|}_{k=1}p_k \log_2 p_k$$ $\text{Ent}(D)$ 值越大越混乱, 当只有一个类别时, `信息熵` 为0 假定通过属性划分样本集 $D$, 产生了 $V$ 个分支节点, $v$ 表示其中第 $v$ 个分支节点. 分支节点包含的样本数越多, 表示该分支节点的影响力越大. 因此可以计算出划分后相比原始数据集D获得的 `信息增益(information gain)` $$\text{Gain}(D,a)=\text{End}(D) - \sum^{V}_{v=1}\frac{|D^v|}{|D|}\text{Ent}(D^v) $$ 信息增益越大, 表示使用该属性划分样本集 $D$ 的效果越好, 因此 `ID3` 算法在递归过程中, 每次选择 **最大信息增益的属性** 作为当前的划分属性. ##### 2. C4.5算法 `ID3算法` 存在偏向于取值数目较多的属性的问题. > 比如样本集 $D$ 被划分为了 $|D|$ 个分支, 每个分支只有1个样本, 信息熵为0, 但对分类没有用处. `C4.5算法` 使用了 `增益率 (gain ratio)` 来选择划分属性, 来避免这个问题. 先使用 `ID3` 计算出信息增益高于平均水平的候选属性, 接着 `C4.5` 计算这些候选属性的增益率. 增益率: $\text{Gain\_ratio}(D,a) = \frac{\text{Gain}(D,a)}{\text{IV}(a)}$, $\text{IV}(a) = -\sum^V_{v=1}\frac{|D^v|}{|D|}\log_2\frac{|D^v|}{|D|}$ 当 $a$ 属性的取值越多时, $\text{IV}(a)$ 的值越大 ##### 3. CART算法 `CART决策树` 使用 `基尼指数 (Gini index)` 来选择划分属性, 基尼指数反映的是从样本集 $D$ 中随机抽取两个样本, 其类别标记不一致的概率, 因此 $\text{Gini}(D)$ 越小越好. 基尼指数: $\text{Gini}(D) = 1 - \sum^{|y|}_{k=1}p_k^2$, 任取2个样本类标不一致的概率, 值越小表示集合越纯 属性 $a$ 的基尼指数: $\text{Gini\_index}(D, a) = \sum^{V}_{v=1}\frac{|D^v|}{|D|}\text{Gini}(D^v)$, 选择基尼指数最小的划分属性 #### 剪枝 不管怎么样的训练集, 决策树总是能很好地将各个类别分离开来, 可能会过于依赖训练样本导致 `overfitting`, `剪枝 (pruning)` 可以解决这一问题 - `预剪枝 (pre-pruning)`: 在构造的过程中先评估,再考虑是否分支 - 通过剪掉决策树的分支, 降低了训练时间开销和过拟合的风险 - 会有欠拟合的风险 - `后剪枝 (post-pruning)`:在构造好一颗完整的决策树后,自底向上,评估分支的必要性 - 保留了更多的分支, 后剪枝策略的决策树性能优于预剪枝 - 训练时间开销大 #### 连续值与缺失值处理 ##### 连续值处理 对于连续值的属性进行离散化处理, 通常使用 `二分法`: 给定样本集 $D$ 与连续属性 $a$, 试图找到一个划分点 $t$ 将样本集 $D$ 在属性 $a$ 上分为 $\leq t$ 与 $>t$ ##### 缺失值处理 一些属性值缺失采取简单剔除, 会造成大量的信息浪费. 属性值缺失需要解决两个问题: 1. 如何选择划分属性 2. 给定划分属性, 若某样本在该属性上缺失值, 如何划分到具体的分支上 解决方案: 1. 通过在样本集 $D$ 中选取在属性 $a$ 上没有缺失值的样本子集, 计算在该样本子集上的 **信息增益**, 最终的信息增益等于该样本子集划分后信息增益乘以样本子集占样本集的比重. 2. 若该样本子集在属性 $a$ 上的值缺失, 则将该样本以不同的权重(每个分支所含样本比例)划入到所有分支节点中. ### 2. CNN卷积神经网络 #### 图像的表达形式 一张输入的图像其实是一个三维的张量, **三个维度分别表示图像的宽, 高和Channel数目**, 彩色图像的每一个像素都是由RGB三个颜色所组成的, 所以3个Channel就分别代表了RGB三个颜色,宽和高表示了这张图像中像素的数目. 将这个三维的张量拉直成一个向量, 每一维里存的数值表示某一个像素在某个颜色上的强度. 使用 `Fully Connected Network` 来实现目标, **随着网络层数增多, 参数也增多, 网络的弹性增强, 更容易出现过拟合问题, 训练的效率也会变低**. 因此 `Fully Collected Network` 并不适合直接拿来处理图像信息, 需要做进一步的简化. 用于图像分类的类神经网络是通过综合检测到的一些重要的 patterns 来进行分类, 因此没必要将一整张图像的每个神经元的输入. 只需要将一小部分输入到神经元就可以检测到某些重要的patterns. ### 感受野 (Receptive Field) 一般在CNN中设置有感受野, 并由一组神经元来处理这个感受野提取的图像信息. 一般感受野是要考虑所有Channels上的信息的. 在描述感受野时, 只要说明宽和高(Kernel Size). #### Example: > 一个蓝色的神经元负责处理左上角感受野中的图像信息为例 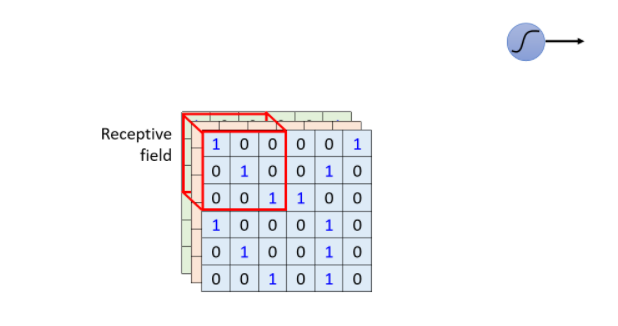 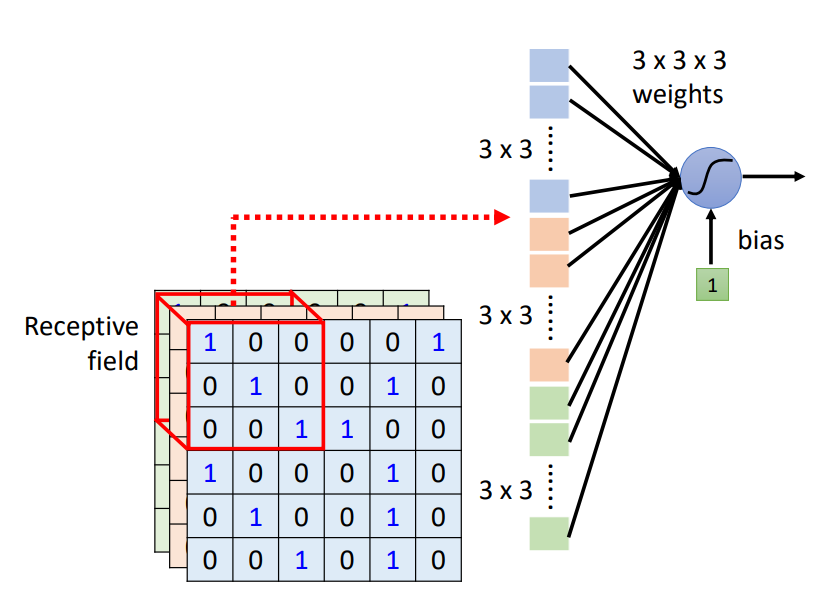 神经元要完成的工作: - 将感受野中 $3 \times 3 \times 3$ 的数值拉直, 变成一个27维的向量, 作为蓝色神经元的输入\ - 神经元给向量中每一个Dimension一个 Weight, 共27个参数 - 再加上 `Bias` 得到输出, 作为下一层神经元的输入 > TODO: CNN剩余部分 ## 本周学习计划 1. 完成Ch.4 决策树的一些公式和习题 2. 神经网络(周志华 《机器学习》 Ch.5) 3. CNN神经网络剩余部分 (李宏毅2021春机器学习课程 Ch.3) 最后修改:2021 年 07 月 26 日 © 允许规范转载 赞 0 如果觉得我的文章对你有用,请随意赞赏