Loading... # 2021.7.5 周记 ## 上一周的学习内容 ### 线性模型 #### 1. 基本形式 通过多个属性描述的示例 $x=(x_1;x_2;\ldots;x_d)$, $x_i$ 是某一属性的取值. `线性模型` 试图通过学习属性的线性组合进行的预测函数 $f(x) = w_1x_1+w_2x_2+\ldots w_dx_d + b$, 向量表示为 $f(x) = w^Tx+b;[w = (w_1; w_2; \ldots; w_d)]$. ##### 优点 - 形式简单、易于建模 - 具有可解释性 - 是非线性模型的基础 #### 2. 线性回归 > 通过学习一个线性模型使其尽可能准确地预测新样本的输出值 ##### 2.1 一元线性回归 即输入只有一元 $f(x_i) = wx_i + b$, 使得 $f(x_i) \simeq y$ 一般通过 `最小二乘法` 求得 $w$, $b$ 1. 均方误差最小化 2. 设置一个代价函数 $E(w,b)$ 3. 分别对 $w$ 和 $b$ 求导, $E$ 为凸函数,导数为 $0$ 即为最优解 最后可以求得 $w$ 和 $b$ $$ w = \frac {\sum^{m}_{i=1}{y_{i}(x_{i}-\bar{x})}} {\sum^{m}_{i=1}{x_{i}^2-\frac{1}{m}(\sum^{m}_{i=1}x_{i})^2}} $$ $$ b = \frac{1}{m}\sum^{m}_{i=1}(y_i-wx_i) $$ 其中, $$ \bar{x} = \frac{1}{m}\sum^m_{i=1}x_i $$ > TODO: 演算结论推导 [^1] ##### 2.2 多元线性回归 一般更多的实际问题是有多个属性描述. 多元问题通常使用矩阵的形式来表示数据. $f(x_i) = w^Tx_i + b$, 使得 $f(x_i) \simeq y$ 通常将具有 $m$ 个样本的数据集表示成矩阵 $X$, 将系数 $w$ 与 $b$ 合并成一个列向量 $$ \hat{w} = (w; b) = \begin{bmatrix} w_1 \\w_2 \\\vdots \\w_d \\b\end{bmatrix} $$ $$ X = \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1d} & 1 \\\vdots & \vdots & \ddots & \vdots & \vdots \\x_{m1} & x_{m2} & \cdots & x_{md} & 1\\\end{bmatrix} =\begin{bmatrix} x_1^T & 1 \\\vdots & \vdots \\x_m^T & 1\\\end{bmatrix} $$ 同样类似 `2.1`, 使用 `最小二乘法` 来对 $w$, $b$ 来进行估计 > TODO: 演算结论推导 [^2] ##### 2.3 对数线性回归 若 $y$ 值并不是线性变化, 而是在指数尺度上变化, 需要将指数曲线投影在一条直线上, 使线性模型的预测值与真实标记联系起来. 即 $\ln y = w^Tx+bx$ 更一般的, 引入 `联系函数 (link function)` $g(\cdot)$, 使 $y = g^{-1}(w^Tx+b)$, 这样得到的模型叫做 `广义线性模型 (generalized linear model)`. `对数线性回归` 是 `广义线性模型` 的一种特殊形式 (即 $g(\cdot) = ln(\cdot)$) #### 3. 对数几率回归 利用 `广义线性模型` 的特征, 通过一个 `联系函数`, 将预测值转化为离散值从而进行分类 通常二分类任务输出为 $\{0,1\}$, 线性模型产生的预测值是实值, 要将值转换为 $0$ 或 $1$. 单位阶跃函数不符合函数连续单调可微的特点, 而使用 `对数几率函数 (sigmoid)`[^3] $$ \ln \frac{y}{1-y} = w^Tx+b $$ 将 $y$ 看做样本为 $0$ 的概率, $(1-y)$ 看做样本为 $1$ 的概率, 则上式实际上使用线性回归模型的预测结果逼近真实标记的对数几率. 因此模型称为 `对数几率回归 (logistic regression)` > TODO: 如何确定w和b [^4] #### 4. 线性判别分析 (LDA) > 基本思想: 将训练样本投影到一条直线上, 使得同类的样例尽可能近, 不同类的样例尽可能远 > > 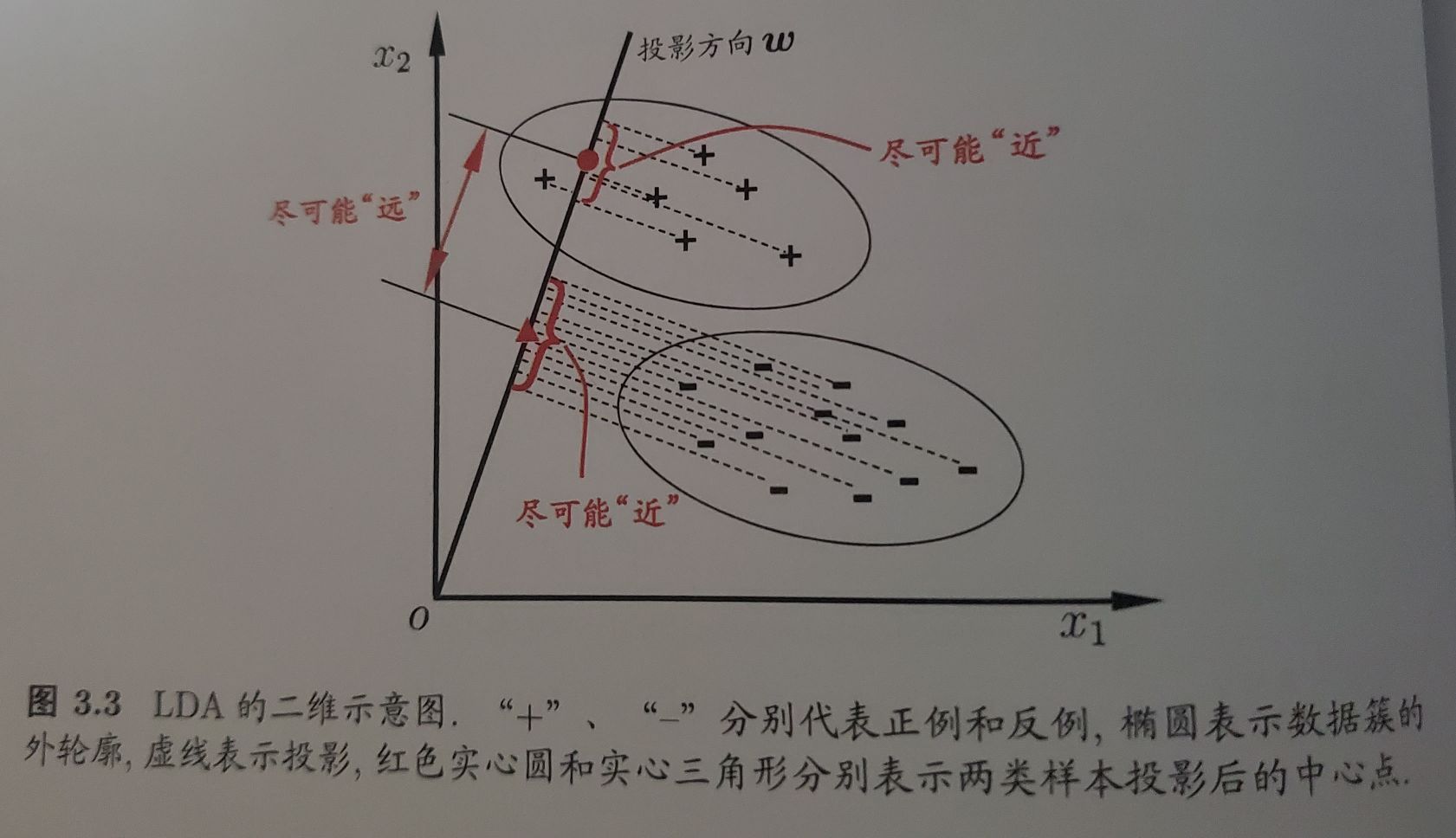 实现这种思想要求不同类样本点投影之间尽可能远. (i.e., 让各类的协方差之和尽可能小, 不用类之间中心的距离尽可能大). 具体实现[^5] #### 5. 多分类学习 > 运用**拆分**的策略, 通过多个二分类学习器来解决多分类问题 拆分策略有三种: - 一对一 (OvO) - 一对其余 (OvR) - 多对多 (MvM) #### 6. 类别不平衡问题 > 分类任务中不同类别的训练样例差别很大的情况, 需要进行相应的处理来平衡这个问题 将平衡问题中 若 $\frac{1}{1-y} > 1$ 则判别为正例的要求 *更改为* 若 $\frac{1}{1-y} > \frac{m^+}{m^-}$ 则判别为正例 ##### 常见类别不平衡的方法 - `欠采样 (undersampling)`: 去除一些正/反例, 使正反例数目接近 - `过采样 (oversampling)`: 增加一些正/反例, 使正反例数目接近 - `阈值移动 (threshold-moving)`: 直接基于原始数据集进行训练, 但是使用 `再缩放` 嵌入到决策过程 `再缩放 (rescaling)`: $\frac{y'}{1-y'} = \frac{y}{1-y} \times \frac{m^-}{m^+}$, 通常 $\frac{m^-}{m^+}$ 估计较为困难 ## 本周学习计划 1. 决策树(周志华 《机器学习》 Ch.4) 2. 推演周志华《机器学习》Ch.3中的一些公式, 并完成TODO和习题 3. 李宏毅2021春机器学习课程 Ch.3 [^1]: 周志华 《机器学习》 P. 54 [^2]: 周志华 《机器学习》 P. 55, 56 [^3]: 6.21周记有提到 [^4]: 周志华 《机器学习》 P. 59 [^5]: 周志华 《机器学习》 P. 60-63 最后修改:2021 年 07 月 26 日 © 允许规范转载 赞 0 如果觉得我的文章对你有用,请随意赞赏