Loading... # 2021.6.28 周记 ## 上一周的学习内容 ### 1. 机器学习的性能度量 `性能度量` (performance measure): 对学习器的泛化性能进行评估, 不仅需要有效可行的实验估计办法, 还需要有衡量模型泛化能力的评价标准. 对比不同模型的能力时, 使用不同的性能度量会导致不同的评判结果. 常用的性能度量是 `均方误差` (mean squared error) 判断模型好坏, 不仅取决于算法和数据, 还取决于任务需求. #### 常用性能度量 ##### 1. 错误率与精度 错误率和精度是分类任务最常用的两种性能度量,适用于二分类和多分类任务 分类错误率定义: $$ E(f;D) = \frac{1}{m}\sum^{m}_{i=1}\mathbb{I}(f(x_i)\neq y_i) $$ 分类精度定义: $$ \begin{aligned} acc(f;D) & = \frac{1}{m}\sum^{m}_{i=1}\mathbb{I}(f(x_i) = y_i) \\ & = 1 - E(f;D) \end{aligned} $$ ##### 2. 查准率, 查全率, F1 错误率合精度并不能满足所有任务需求. 对于二分类问题可以将样例根据类别划分为 `真正例 (true positive)`, `假正例 (false positive)` , `真反例 (true negative)`, `假反例 (false negative)` | 真实情况 \ 预测结果 | 正例 | 反例 | | :---: | :----: | :----: | | 正例 | $TP$ | $FN$ | | 反例 | $FP$ | $TN$ | 查准率定义: $$ P = \frac{TP}{TP+FP} $$ 查全率定义: $$ R = \frac{TP}{TP+FN} $$ 查准率和查全率是一对矛盾的度量. 一般 $P$ 越高, $R$ 则越低; 反之相反. ###### P-R曲线 以查准率为横坐标, 查全率为纵坐标绘制的曲线. ###### 平衡点 (Break-Even Point, BEP) 是当 $P=R$ 时的取值. 如 Pic 2.3 [^1], $BEP_A > BEP_B$, 可以认为学习器 $A$ 优于 $B$. 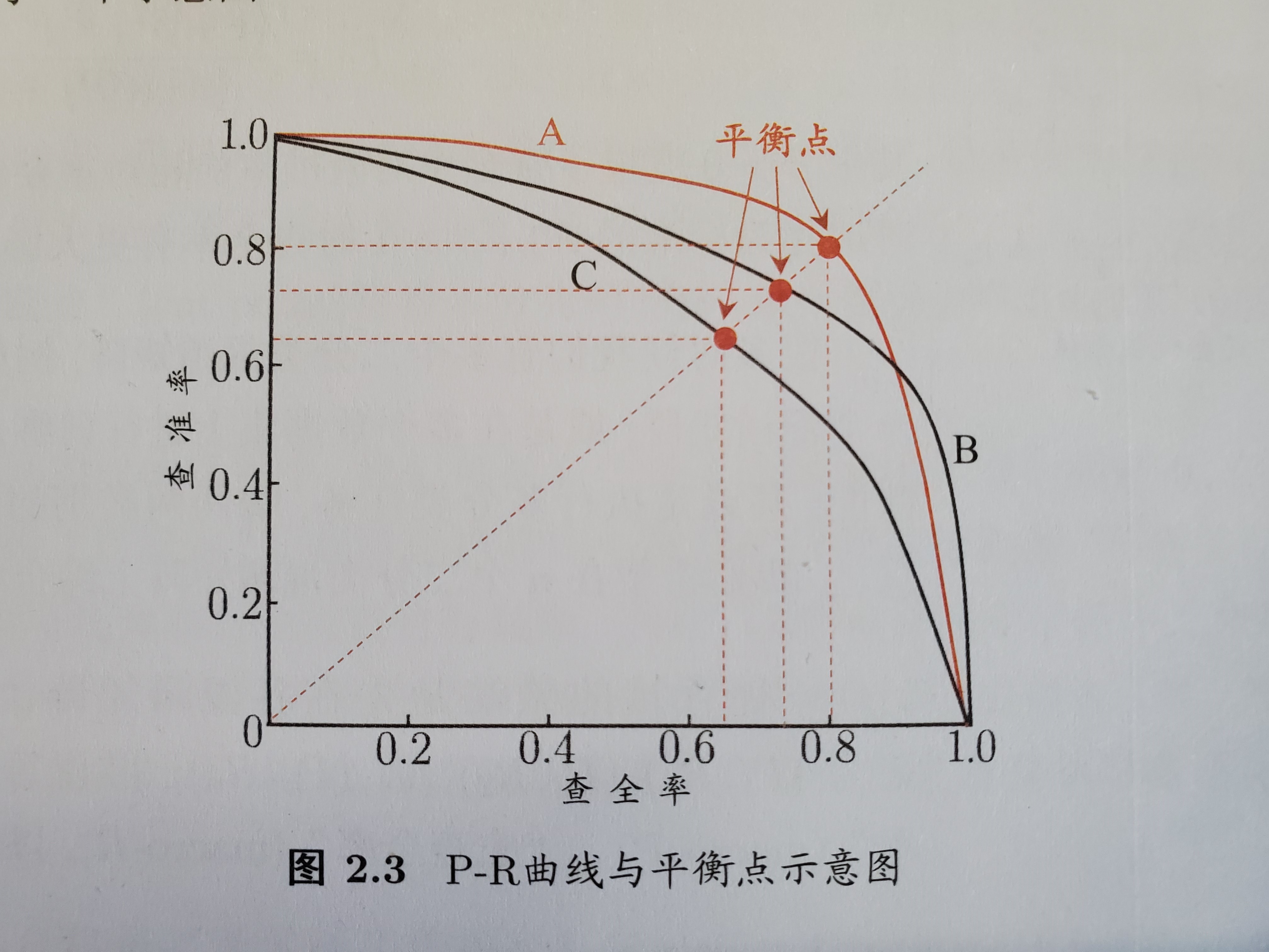 ###### $F_1$, $F_\beta$ 度量 $F_1$ 是基于查准率和查全率的调和平均定义的 $$ \frac{1}{F1} = \frac{1}{2} \cdot (\frac{1}{P} + \frac{1}{R}) $$ $$ F1 = \frac{2 \times P \times R}{P + R} = \frac{2 \times TP}{样例总数 + TP - TN} $$ 通常应用会对查准率或查全率有偏好, 使用 $F_\beta$ 进行度量 (基于 $P$, $R$ 的加权调和平均) $$ \frac{1}{F_\beta} = \frac{1}{1+\beta^2} \cdot (\frac{1}{P} + \frac{\beta^2}{R}) $$ $$ F_\beta = \frac{1+\beta^2 \times P \times R}{(\beta^2 \times P+R)} $$ 其中, $\beta > 0$ 度量了查全率对查准率的相对重要性. $\beta = 1$ 退化为标准 $F1$; $\beta > 1$ 偏好查全率, $\beta<1$ 偏好查准率 ###### 根据P-R曲线比较学习器性能 1. 若一个学习器 $A$ 的 `P-R曲线` 被另一个学习器 $B$ 曲线完全包住, 确定 $B$ 性能优于 $A$ 2. 若两个学习器 $A,B$ 的 `P-R曲线` 存在交集, 可以比较面积 3. 基于 `BEP` 衡量性能. `BEP` 越大, 性能越好 4. 基于 `F1`, `$F_\beta$` 度量 ##### 3. ROC, AUC ###### ROC (Receiver Operating Characteristic) 根据学习器的预测结果对样例进行排序, 按此顺序逐个把样本作为正例进行预测, 每次计算出假正例率和真正例率, 以 `真正例率 (True Positive Rate)` 为纵轴, `假正例率 (False Positive Rate)` 为横轴绘制的图为 `ROC` $$ TPR = \frac{TP}{TP + FN} $$ $$ FRP = \frac{FP}{TN + FP} $$ 其中, 点 $(0, 1)$ 为所有正例排在所有反例之前的理想模型 ###### AUC (Area Under ROC Curve) ROC曲线下的面积为AUC $$ AUC = \frac{1}{2}\sum^{m-1}_{i=1}(x_{i+1}-x_i)\cdot(y_i+y_{i+1}) $$ > 设当前点为 $(x_i, y_i)$, 若 $(x_{i+1}, y_{i+1})$ 为真正例,那么横坐标不变, 纵坐标加常数, 则该项加0; 若 $(x_{i+1}, y_{i+1})$ 为假正例, 那么横坐标加常数, 纵坐标不变, 则 $\frac{1}{2}\sum^{m-1}_{i=1}(x_{i+1}-x_i)\cdot(y_i+y_{i+1})$ 为当前矩形的面积. 损失函数定义为: $$ l_{rank} = \frac{1}{m^{+}m^{-}\sum_{x^+ \in D^+}}\sum_{x^- \in D^-}(\mathbb{I}(f(x^+)<f(x^-)) + \frac{1}{2}\mathbb{I}(F(x^+)=f(x^-))) $$ > TODO: 没搞懂 ##### 4. 代价敏感错误率与代价曲线 代价敏感错误率即对错误情况加权值. 根据ROC曲线, 将ROC曲线上每一个 $(FPR,TPR)$, 在代价平面上绘制一条从 $(0,FPR) \to (1,TPR)$ 的线段, 所有线段下的总面积为该条件下的期望总体代价. ### 2. 机器学习的比较检验 #### 机器学习中的性能比较复杂的原因 1. 希望比较的是泛化性能, 然而通过实验评估获得的只是测试集上的性能, 两者对比结果可能未必相同 2. 测试集上的性能与测试集本身选择有很大的关系, 不同的测试集会得到不同的结果 3. 很多机器学习算法本身有一定的随机性, 即便用相同的参数设置, 在同一个测试集多次运行, 结果也可能不同 #### 几种假设检验的方法 ##### 1. 假设检验 由于泛化错误率与测试错误率比较接近, 因此可以根据测试错误率估推出泛化错误率的分布. 泛化错误率 $\epsilon$: 学习器被测得测试错误率为 $\hat{\epsilon}$ 的概率 $$ P(\hat{\epsilon}, \epsilon) = \begin{pmatrix} m \\ \hat{\epsilon} \times m \end{pmatrix} \epsilon^{\hat{\epsilon} \times m} (1-\epsilon)^{m - \hat{\epsilon} \times m} $$ 可以得知 $P(\hat{\epsilon}, \epsilon)$ 在 $\epsilon = \hat{\epsilon}$ 时最大, $|\epsilon - \hat{\epsilon}|$ 增大时 $P(\hat{\epsilon}, \epsilon)$ 减少, 这符合二项分布. 使用二项检验, 假设 $\epsilon \leq \epsilon_0$, 则在 $1-\alpha$ 的概率内所能观测到的最大错误率为 $$ \bar{\epsilon} = \min \epsilon \ \text{s.t.} \ \sum^{m}_{i=\epsilon_0 \times m+1} \begin{pmatrix} m \\ i \end{pmatrix} \epsilon^{i}(1-\epsilon)^{m-i} < \alpha $$ > `s.t.` 为 `subject to` 的缩写, 使左式子在右边条件满足时成立 若测试错误率 $\hat{\epsilon} < \epsilon$, 根据二项检验可得出结论: 在 $\alpha$ 的显著度下, 假设 $\epsilon \leq \hat{\epsilon}$ 不能被拒绝 (i.e. 能以 $1-\alpha$ 的置信度认为学习器的泛化错误率不大于$\epsilon_0$ ). ##### 2. 交叉t检验 对两个学习器 $A$ 和 $B$, 使用 `k折交叉验证法` 得到的测试错误率分别为 $\epsilon_i^A$ 和 $\epsilon_i^B$. 对 `k折交叉验证` 产生的 $k$ 对测试错误率: 先对每对结果求差, $\Delta_i = \epsilon_i^A - \epsilon_i^B$. 若两个学习器性能相同,则差值均值班为零. 对 ``学习器 $A$ 与 $B$ 性能相同`` 这个假设做 `t检验`,在显著度 $\alpha$ 下,若变量为:$\tau_t = |\frac{\sqrt{k}\mu}{\sigma}|$, 小于临界值则假设不能被拒绝(i.e. 两个学习器 $A$, $B$ 的性能没有显著差差别); 否则可认为两个学习器的性能有显著差别, 平均错误率较小的那个学习器性能较优. ##### 3. McNemar检验 ##### 4. Friedman检验与Nemenyi后续检验 ### 3. 类神经网络的几个要点 #### 当模型loss较大的时候, 如何进行调整 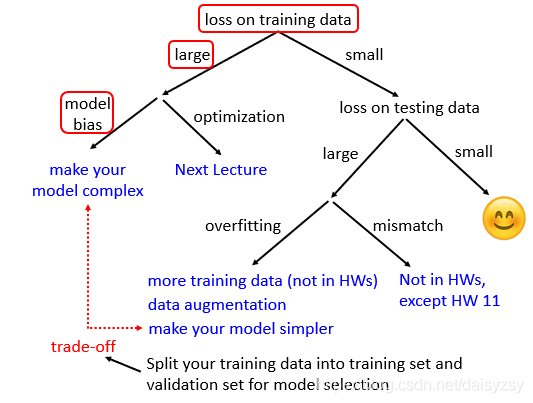 ##### Training loss 较大的情况 ##### 1. Model bias - 模型本身带来的偏差 模型过于简单, 无法找到某一个假设使得模型很好的拟合训练数据, 这个时候应当增加模型的复杂性, 让模型更复杂一些 解决办法: - 添加更多的特征 - 添加更多的网络层 - 选择一个更复杂的model ##### 2. Optimization Issue - 模型没有调优至最佳 训练过程中模型陷入局部最优, 在现有的假设空间内算法调优不仅没有找到最优解 ##### 区分是 `Model bias` 还是 `Optimization Issue` 在现有模型上先增加模型的复杂度, 比如多一些层, 然后看看加了模型复杂度之后, 模型在训练集上的training loss是不是有所下降. 若下降了则是 `Model bias`, 上升了则是 `Optimization Issue` #### training loss比较小, 但是testing loss比较大 ##### 1. Overfitting 解决方法: - 增加训练数据, 数据增强 - 给与模型一些限制, 缩小假设空间 ##### 2. Mismatch 训练集的数据分布和测试集的数据分布不一样导致 解决办法: - 实际过程中遇到这种情况,调整训练集和测试集即可 ## 本周学习计划 1. 机器学习的几类线性模型.(周志华 《机器学习》 Ch.3) 2. CNN模型 (李宏毅2021春机器学习课程 Ch.3) ## BTW 我高估了我的学习速度 :slightly_frowning_face: [^1]: 周志华 《机器学习》 P. 35 最后修改:2021 年 07 月 26 日 © 允许规范转载 赞 0 如果觉得我的文章对你有用,请随意赞赏