Loading... ## 上一周的学习内容 ### 1. Transformer #### 1.1 Sequence-to-sequence (seq2seq) ##### 作用 输入一个序列, 输出一个序列. 输出的长度由模型决定. ##### 使用方向 - 语音辨识 - 机器翻译 - 语音翻译 - Text-to-speech(TTS) - Multi-label classification - Object detaction #### 1.2 Encoder > 输入一组向量, 输出一组同样长度的向量 (除了 `Self-attention`, 还可以使用 `RNN` 或 `CNN`). > > 如输入 $X(x^1,x^2,x^3,x^4)$, 输出 $H(h^1,h^2,h^3,h^4)$ `Encoder` 中, 输入需要经过多个 `Block` 的处理得到输出 ##### 原理 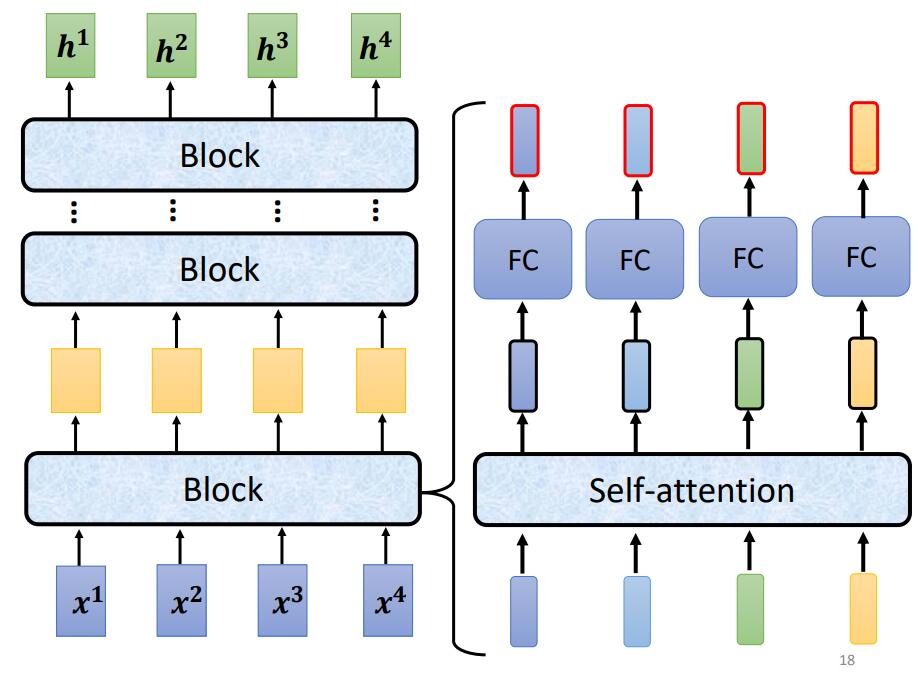 如 `Pic 1`: 1. 对输入 $X(x^1, x^2, x^3, x^4)$ 进行一次 `Self-attention`; 2. 将 `Self-attention` 的输出丢入 `Fully connect` 的 `Fead Forward Network` 中, 输出结果. > 1个 `Block` 做的事, 是好几个Layer在做的事情, 因此 `Block` 并不是 `Neural Network` 中的一层. ##### `Block` 具体过程 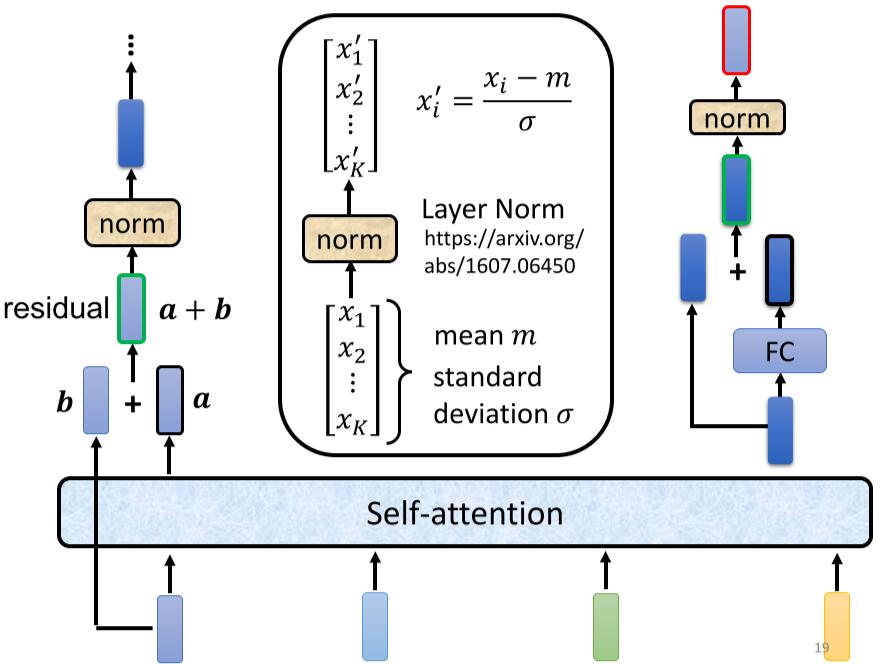 > - `Residual Connection`: 将输出的向量加上之前输入的向量作为新的输出 > - `Layer Normalization`: > 1. 输入一个向量, 计算其平均值 $m$, 标准差 $\sigma$ > 2. 不同于 `Batch Normalization` > - `Batch Normalization`: 对不同的样例, 不同特征的同一维度去计算 $m$ 和 $\sigma$ > - `Layer Normalization`: 对同一样例, 同一特征的不同维度去计算 $m$ 和 $\sigma$ > 3. 根据公式 $x_i'=\frac{x_i-m}{\sigma}$ 得到新的向量 如 `Pic 2`: 1. 对向量位置有要求, 需要先对输入进行 `Position Embedding` 2. 对输入向量做 `Self-attention`, 得到 $a$ 3. 做 `Residual Connection`, 得到 $(a+b)$ 4. 对向量 $(a+b)$, 做 `Layer Norm` 5. 再对上一步得到的结果, 在做 `Fully connect` 6. 再对上一步的结果做 `Residual` 和 `Layer Norm`, 得到该 `Block` 的输出 重复多次 `Block` 过程. #### 1.3 Decoder > `Decoder` 完成模型的最终输出 ##### Autoregression (自回归, AT) ###### 过程 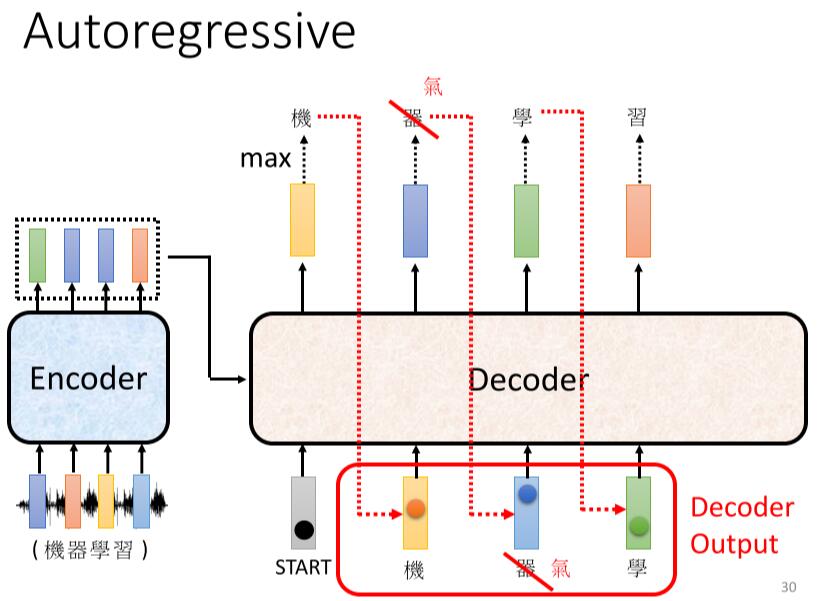 1. 开始给定一个Begin标记(``BOS``) 2. 输入向量经过 `Decoder` 得到输出的向量 3. 将输出的向量, 经过 `Soft-max` 得到每个字的分数, 将最高分数的字符作为结果 4. 将该次生成的结果作为下一次的输入, 重复第2步, 直到遇到End标记(``EOS``) > `Pic 3` 的 `Decoder Output` 可能产生 `Error Propagation`, 即一步错步步错. ##### `Autoregression` 的 `Decoder` 结构 在 `Decoder` 中, 通常使用 `Masked Multi-head Self-attention`. 原本的 `Self-attention` 需要考虑所有输入向量才能计算出 $(q,k,v)$, 之后才能得到输出向量. 而 `Masked Multi-head Self-attention` 只考虑自己与自己之前的向量即可, 例如需要输出向量 $b^3$ 时, 只需要考虑 $a^1,a^2,a^3$ 所产生的 $(q,k,v)$, 而无需考虑 $a^4$ > **Q1: 为什么使用 `Masked Multi-head Self-attention`?** > > 在 `AutoRegression` 中, 输出时一个个根据前一次的输出所产生的, 并不会考虑之后的事情. > > **Q2: 什么时候Encoder停下来?** > > 准备一个特殊符号 ``EOS``, 当结束时, 让End标记的几率最大时, 结束Encoder. 即让机器自己训练决定何时该结束. ##### Non-autoregression (NAT) `NAT` 与 `AT` 的差别, 在于AT需要上一步的输出作为下一步的输入, 并一步步这样循环. 而 `AT` 则直接一次性输入, 直接得到输出. ###### 如何决定 NAT 输出的长度 有两种思路: - 另外学习一个Classifier, 输入 Encoder 的输入, 输出一个值表示该Decoder输出的长度; - 设定一个较大上限值, 观察何处出现End标记, 丢弃End标记之后的所有输出. ###### NAT 优缺点 - 优点: 平行处理, 可以控制输出的长度 - 缺点: 效率与性能不如 `AT` #### 1.4 Encoder 与 Decoder 之间的通信 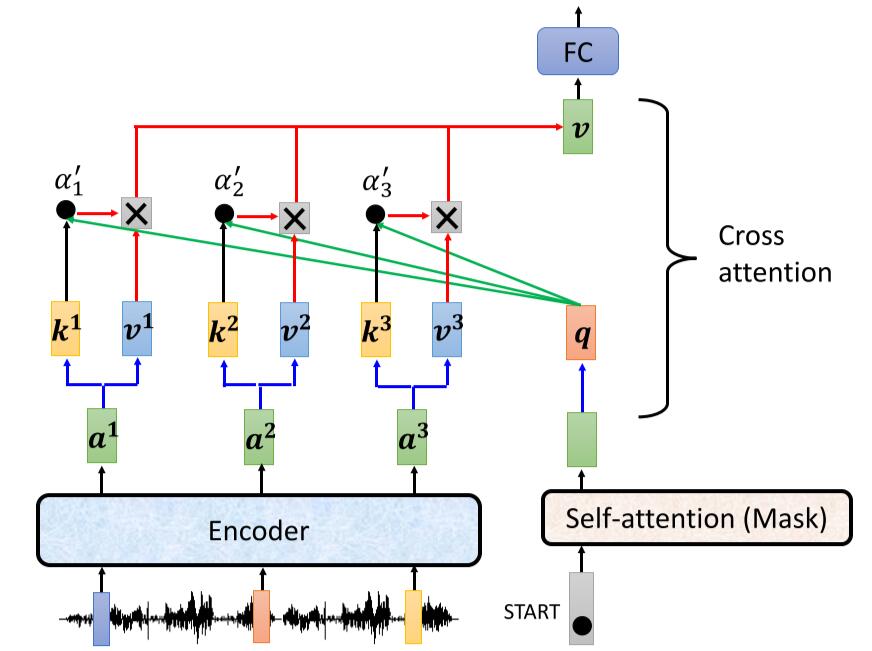 1. 在 Encoder 部分, 输入一组向量后输出了 $(a^1, a^2, a^3)$ 2. 在 Decoder 部分, 得到一个输入(如 ``BOS``), 经过 `Masked Multi-head Self-attention` 得到向量, 乘上矩阵做 `Transformer`, 得到 query - $q$ 3. 在 Encoder 部分, 各个向量一次产生 key - $(k^1, k^2, k^3, \cdots)$, 将 $k$ 与 $(k^1, k^2, k^3, \cdots)$ 进行计算得到分数 - $(\alpha^1, \alpha^2, \alpha^3, \cdots)$, 进行 `Soft-max`, `Norm` 等操作, 得到 $(\alpha_1', \alpha_2', \alpha_3', \cdots)$ 4. 在 Encoder 部分, 产生向量 $(a^1, a^2, a^3, \cdots)$ 的 value - $(v^1, v^2, v^3, \cdots)$, 与 $(\alpha_1', \alpha_2', \alpha_3', \cdots)$ 相乘. $v = \sum_h (v^i\alpha_i')$ 5. 将 $v$ 做 `Fully-connection`, 丢入 Network 进行接下来的处理 #### 1.5 Training ##### 训练方式 当将 ``BOS``丢入 Encoder 时, 希望将输出与字符 $x$ 越接近越好. $x$ 会被表示成一个 `one-hot vector`, 只有 $x$ 对应的那个维度是 $1$, 其余皆为 $0$. 此时 Decoder 输出一个 `Distribution`(几率的分布), 此时希望纪律分布与该 `one-hot vector` 越接近越好. > 即计算输出的 `Ground Truth` 与 `Distribution` 之间的 `Cross-entropy`, 越小越好. 近似于分类问题. 在 Decoder 训练过程中, 在输入的时候基于其正确答案, 这个过程称为 `Teacher Forcing`. 在实际使用模型时, Decoder 因为仅仅时看见自己的输入, 中间存在 Mismatch. ##### 解决Mismatch的一些方法 - Copy Mechanism - Summarization - Guide-attention - Scheduled Sampling --- ### 2. 支持向量机 #### 2.1 间隔与支持向量 给定样本集 $D$, 分类学习基本思想是在样本空间中找到一个划分超平面, 将不同样本分开. 划分超平面可以通过线性方程表示: $$ w^Tx+b=0 $$ > 与 $y$ 无关, 是特征空间中的一条线. 将超平面可以记为 $(w, b)$, 则样本空间任意点到超平面 $(w, b)$ 的距离为 $$ r =\frac{\lvert w^Tx+b \rvert}{\lVert w \rVert} $$ 根据缩放变换, 将超平面上的点标记为 $1$; 之下的点标记为 $-1$. (即让 $|w^Tx+b|=1$) $$ \begin{cases} w^Tx_i+b \geq +1, y_i=+1 \\ w^Tx_i+b \leq -1, y_i=-1 \\ \end{cases} $$ 距离超平面**最近**的训练样本使上式的等号成立, 这些样本点称为`支持向量(Support vector)`. 两个异类的支持向量到超平面的距离和被称为 `间距(margin)`: $$ \gamma = \frac{2}{\lVert w \rVert} $$ 找到最大间隔的划分超平面, 就是找到满足约束的 $w$ 和 $b$, 使 $\gamma$ 最大. $$ \begin{aligned} &\min_{w,b} \frac{1}{2} \lVert w \rVert^2 \\ & \text{s.t.} y_i(w^Tx_i+b) \geq 1, i=1,2,3,\ldots,m. \end{aligned} \tag{2.1} $$ 即 `支持向量机(Support Vector Machine, SVM)` 的基本型. #### 2.2 对偶问题 式2.1使凸二次规划问题, 可以直接进行求解, 但复杂度较高. 对式2.1使用拉格朗日乘子法可以得到 `对偶问题(Dual Problem)`, 对式2.1的每个约束添加拉格朗日乘子 $\alpha_i \geq 0$, 问题可以写成: $$ L(w,b,\alpha)=\frac{1}{2}\lVert w \rVert ^2 + \sum^m_{i=1}\alpha_i(1-y_i(w^Tx_i+b)) $$ > 式2.1到上面的式子并非拉格朗日乘子法, 因为2.1是个不等式, 需要满足KKT条件 令 $L$ 对 $w,b$ 求偏导: $$ w=\sum^m_{i=1} \alpha_i y_i x_i $$ $$ 0 = \sum^m_{i=1} \alpha_i y_i $$ 代入 $L$ 消去 $w, b$. 得到了式2.1的对偶问题 $$ \max_\alpha \sum^m_{i=1} \alpha_i - \frac{1}{2} \sum^{m}_{i=1}\sum^{m}_{j=1} \alpha_i \alpha_j y_i y_j x_i^T x_j $$ > 运算过程: > > $$ > \begin{aligned} L(w,b,\alpha) &= \frac{1}{2}\lVert w \rVert ^2 + \sum^m_{i=1}\alpha_i(1-y_i(w^Tx_i+b)) \\ &= \frac{1}{2} w^Tw + \sum_i \alpha_i(1-y_i(w^Tx_i+b)) \\ &= \frac{1}{2} (\sum_i \alpha_i y_i x_i)^T (\sum_i \alpha_i y_i x_i) + \sum_i \alpha_i(1-y_i(\sum_j \alpha_j y_j x_j)^Tx_i+b) \\ &= \sum \alpha_i - \frac{1}{2} (\sum_i \alpha_i y_i x_i)^T (\sum_i \alpha_i y_i x_i) \\ &= \sum \alpha_i - \frac{1}{2} \sum^{m}_{i=1}\sum^{m}_{j=1}\alpha_i \alpha_j y_i y_j x_i^T x_y \end{aligned} > $$ 解出 $\alpha$ 即可求出 $w, b$ 得到模型. $$ \begin{aligned} f(x) &= w^Tx+b \\ &= \sum_{i=1}^m \alpha_i y_i x_i^T x + b \end{aligned} \tag{2.2} $$ 对训练样本 $(x_i, \hat{y_i})$, 总有 $\alpha_i=0$ 或 $y_if(x_i)=1$ - 若 $\alpha_i=0$, 则不会对 $f(x)$ 有任何的影响 - 若 $y_if(x_i)=1$, 则对应的样本点在最大间隔上, 是一个支持向量. 因此支持向量的大部分训练样本无需保留, 最终模型仅与支持向量有关. 求解式子2.2可以使用 `SMO算法` 求解 #### 2.3 核函数 2.1 和 2.2假设了训练样本是线性可分的. 若无法可分, 则需要将原始的二位空间映射到一个合适的三维空间. > 如果原始空间是有限维, 则一定存在一个高维空间使样本可分 可以设 $\phi(x)$ 是 $x$ 映射后的特征向量, 通常计算 $\phi(x)$ 是很困难的, 可以通过 `核函数(kernal function)` 来避开障碍, 例如: $$ \kappa(x_i, x_j) = \langle \phi(x_i), \phi(x_j) \rangle = \phi(x_i)^T\phi(x_j) $$ 这时候的对偶问题就会变为: $$ \max_\alpha \sum^m_{i=1} \alpha_i - \frac{1}{2} \sum^{m}_{i=1}\sum^{m}_{j=1} \alpha_i \alpha_j y_i y_j \kappa(x_i, x_j) $$ 原分类函数会变为: $$ f(x) = \sum^n_{i=1}\alpha_i y_i \kappa(x_i, x_j) + b $$ 因此, 在线性不可分问题中, 核函数的选择成了支持向量机的最大变数, 若选择了不合适的核函数, 则意味着将样本映射到了一个不合适的特征空间, 则极可能导致性能不佳. 同时, 核函数需要满足以下这个必要条件  yinwei核函数的构造十分困难, 通常我们都是从一些常用的核函数中选择:  核函数有以下几种特性: 1. 核函数 $\kappa_1$, $\kappa_2$ 对于任意正数 $\gamma_1$, $\gamma_2$ 的线性组合 $\kappa_1 \gamma_1+\kappa_2 \gamma_2$ 也是核函数 2. 核函数 $\kappa_1$, $\kappa_2$ 的直积 $\kappa_1 \bigotimes \kappa_2 = \kappa_1(x,z)\kappa_2(x,z)$ 也是核函数 3. 核函数 $\kappa_1$, 对于任意函数 $g(x)$, $\kappa(x,z) = g(x)\kappa_i(x,z)g(z)$ 也是核函数 #### 2.4 软间隔支持向量机 之前都是假定样本集在样本空间中是线性可分的, 但是通常现实任务很难确定合适的核函数使其线性可分. 即使恰好找到了核函数也有可能造成过拟合. 缓解问题的一个办法是允许向量机在一些样本上出错. - `硬间隔(Hard margin)`: 所有样本必须划分成功; - `软间隔(Soft margin)`: 允许某些样本不满足约束, 即 $y_i(w^Tx_i+b) \geq 1$ 在最大化间隔的同时, 应当使不满足的样本尽可能的少. 优化目标可以写为 $$ \min_{w, b} \frac{1}{2} \lVert w \rVert^2 + C \sum_{i=1}^m l(y_i(w^Tx_i+b) - 1)\tag{2.3} $$ > $l(z)$ 为损失函数, 常见的损失函数有: > > - 0/1损失 > - hinge损失 > - 指数损失 > - 对率损失 - 当 $C$ 为无穷大时, 所有样本均满足约束条件 - 当 $C$ 取有限值时, 允许部分样本出现误差(不满足约束) 更通常的, 将式2.3写成 $$ \min_{f} \Omega(f)+C\sum^m_{i=1} l(f(x_i),y_i) $$ 其中: - $\Omega(f)$ 称为 `结构风险(structural risk)`, 用于描述模型 $f$ 的某些性质 - $\sum^m_{i=1} l(f(x_i),y_i)$ 称为 `经验风险(expirical risk)`, 用于描述数据的契合程度 - $C$ 用于对两者进行折中 ## 本周学习计划 1. 周志华 《机器学习》 Ch.7 贝叶斯分类器 2. 李宏毅2021春机器学习课程 Ch.6 Generative Model 3. 看2篇论文 最后修改:2021 年 07 月 26 日 © 允许规范转载 赞 0 如果觉得我的文章对你有用,请随意赞赏