Loading... <button class="btn m-b-xs btn-info btn-addon" onclick='window.open("https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CJFD&dbname=CJFDLAST2021&filename=RJXB202103016&v=ed6oAmHPQrLrkwPq26FafQIL1sGsEt%25mmd2BuBZRWQMcnZNcdFSfnDqvJJfbwfS9B7Ss%25mmd2F","_blank")'><i><i data-feather="external-link"></i></i>CNKI</button> > **标题**: 多尺度时序依赖的校园公共区域人流量检测 > **作者**: 谢贵才, 段磊, 蒋为鹏, 肖珊, 徐一凡 > **通讯作者**: 段磊 (leiduan@scu.edu.cn) > **单位**: 四川大学 ## Abstract 通过基于深度学习的多尺度时序卷积网络MSCNN, 通过流量数据的中短时依赖, 长时周期数据的获取和多尺度时序模式特征的重标定, 以对任意时段的人流量进行预测. ### Some Question > 然而, 由于校园管理需求, 如节假日和教学安排等因素, 使得校园公共区域人流量预测问题颇具挑战性. 1. 具有哪些挑战 2. 如何解决这些挑战 3. 现有人流量预测模型有什么缺点 > 提出一种基于深度学习的多尺度时序卷积网络MSCNN(multi-scale temporal patterns convolution neural networks), 实现人流量时序数据中短时依赖、长时周期模式的获取和多尺度时序模式特征的重标定, 以对任意时段人流量进行预测. 4. 什么是MCSCNN, 与CNN的差别在哪里, 为什么要使用MSCNN 5. MSCNN中, 多尺度时序是什么, 多尺度中的尺度是哪些 6. 中短时依赖,长时周期模式的获取,多尺度时序模式特征的重标定 这三者是什么, 是如何实现的, 它们对于MSCNN有哪些帮助 7. MSCNN模型是怎样定义的, 实现过程是怎样的 > 通过在真实校园环境数据集以及公开数据集上的实验, 验证了MSCNN模型的有效性和执行效率. 8. 数据集的包含了哪些内容 9. 通过何种方法验证模型的有效性和执行效率 10. MSCNN模型存在的问题和改进之处 ## Introduction ### 人流量预测所遇到的困难 从技术上来讲, 校园公共区域进行人流量预测主要有以下三个挑战: 1. 师生前往公共区域的行为具有不确定性; 2. 在一些日子人流量的差异可能会非常明显, 比如考试周, 节假日等等; 3. 不同类型的公共区域人流量具有相关性, 同一时刻一个区域的人流量会影响到另一个区域的人流量. 以上的这三点, 都会对人流量预测产生不确定的因素. ### 当前发展 对于人流量相关属性的预测可以看作是 **时序预测问题**. 关于时序预测问题, 早期的研究可以分为两种方法: - 早期的时序预测模型 - 传统的机器学习方法 其中, 早期的时序预测方法只能针对相对平稳且呈线性变化的数据进行预测, 存在很大的局限性; 而传统的机器学习方法虽然可以建模, 但是无法捕捉短时依赖和长时周期模式, 十分依赖特征工程. 当前深度学习技术也可以解决相当的时序任务, 如神经卷积网络和循环神经网络. 但是目前深度学习对于同时捕获不同尺度的时序模式和变量局部依赖性仍然需要探索. ### 解决方案 通过基于深度学习的多尺度时序卷积网络MSCNN来解决该问题. MSCNN通过以下3个模式组件来解决上面提出的三个挑战: - 短时模式组件 - 长时模式组件 - 融合组件 ## 综述 人流量预测问题的核心在于如何有效捕获人流量序列中的短时依赖和长时周期时序模式,并考虑多区域之间的相互依赖关系. 目前时序预测主要有基于统计学方法和基于深度学习方法两种. ### 基于统计学的方法 基于统计学的方法主要包括回归模型和非参数模型两种. - 回归模型 `差分滑动平均自回归模型ARIMA` 可以对数据进行描述和预测, 适用于指数平滑技术, 具有足够的灵活性. 例如 `线性支持向量回归SVR` 也可以将时序预测问题看作具有时间变化参数的 `标准回归问题` - 非参数模型 `高斯过程模型` 是一种在连续域上模拟分布的非参数模型. 但是设计矩阵求逆运算, 增加计算复杂度. ### 基于深度学习的方法 - `ARIMA模型` 和 `多层感知机MLP` 结合 - `CNN` 从输入序列数据中提取平移不变的局部模式作为特征进行多做序列分类 - `动态玻尔兹曼机` 和 `循环神经网络` 结合, 捕捉时序序列的依赖关系, 对多元时序数据进行预测 - `长短时记忆网络LSTM` 和 `门控循环网络GRU` 作为CNN的变体, 在时序数据分析具有广泛应用. 但是天然存在梯度消失问题, 会产生较高的计算代价 ### 两种方法存在的问题 基于统计学的研究通常不能针对多个时序变量同时进行预测. 而基于深度学习方法无法直接对区域人流量数据的多尺度模式同时进行考虑, 预测结果不够准确. ## 实验设计 MSCNN分为了3个模组: - 短时模式组件 - 长时模式组件 - 融合组件 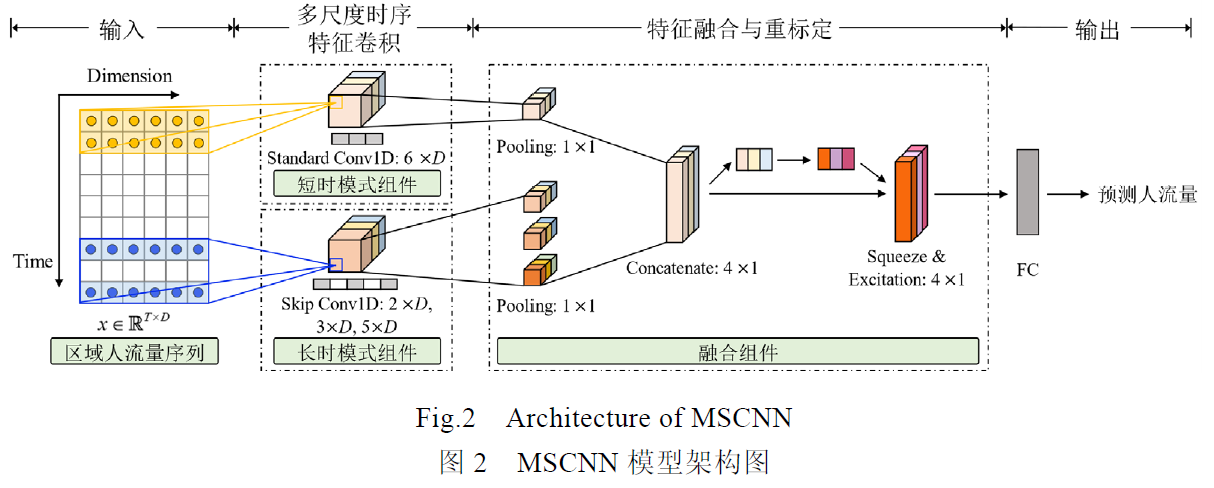 ### 短时模式组件 短时模式组件主要捕获短时时序序列. 即与预测时段直接相邻的一段历史事件序列片段. 通常来讲, 某区域的上一时段人流量会对下一时段人流量产生很大影响. 短时模式组件使用 `CNN卷积运算` 捕获 短时时序片段模式(挑战1) 和 不同区域间存在的局部依赖问题(挑战3) #### 实现 我们知道 `卷积核` 的大小反映了一个单元的状态有多大范围内的临近单元所决定. 每个卷积都是一种特征提取方式, 就像一个筛子, 符合条件 (激活值越大越符合条件) 的部分筛选出来.  通过设置 $K$ 个大小为 $6 \times D$ 的卷积核对短时时序片段 $F_S$ 进行卷积操作. $\boldsymbol{F}=(\boldsymbol{X}_1, \boldsymbol{X}_2, \cdots)\in\mathbb{R}^{T \times D}$ 表示 $D$ 个区域在 $T$ 个时刻的人流量序列. $$ H_k^C = \text{ReLU}(W_k^C*\boldsymbol{F}_S+b_k^C) $$ 可以捕获短时行为时序模式和变量之间的局部依赖性. > **Conv1D**: > 区别于Conv2D中kernal向输入的 $x$, $y$ 两个方向进行移动 Conv1D 只会向一个方向进行移动. > Conv2D通常用于图的CNN, Conv1D则通常用于文本分类. > 图的解释: >  > 在图的**左半部分**: > 假设图中区域人流量序列输入矩阵大小为 $9 \times 6$, 设置 kernal size 为 $3$. 以时间从上至下进行一边扫描, 卷积得到了一个长度为 $7 \times 1$ 的输出向量. > 在图的**右半部分**: > Input层经过卷积得到Conv1D层的卷积结果, 最后将 $K$ 个kernal输出的结果合并得到Output层. ### 长时模式组件 长时模式组件主要捕获长时周期的时序序列. 即与预测时段具有相同星期属性的片段组成. 通常来说, 每个周末的周三人流量都会非常相似. 论文通过Dilated卷积来实现捕获长时周期模式, Dilated卷积通过设置skip跳跃参数实现获得长时周期的捕获. MSCNN通过3中skip卷积核来捕获特征: 2-skip, 3-skip, 5-skip. 具体步骤类似于短时模式组件. > **Dilated Convolution**: > 空洞卷积(膨胀卷积, Atrous Convolution), 作用是扩大感受野和捕获多尺度上下文信息. > 缺点是容易造成: 1. 局部信息丢失; 2. 远距离获取的信息没有相关性. > > 在这篇论文里, 由于设置了短时模式组件, 所以并没有局部信息丢失的问题; 同时, 由于问题中预测时段这个问题中本身就具备一定的相关性, 因此远距离获取的信息没有相关性这个缺点并不会很大影响预测准确度. ### 融合组件 由两个子组件组成: - 将短时模式与长时模式捕获到的特征进行融合 - 特征重标定 #### 多尺度时序模式特征融合 目的是将短时模式与长时模式组件获取的特征信息进行融合. 因为4种kernal的设置不同, 所以输出结果的维度也不相同. 因为每种卷积核都使用了 $K$ 种kernal数目, 所以可以用 Global Average Pooling 来进行进行采样. 最终得到4个维度相同的 $K \times 1 \times 1$ 的采样结果, 拼接后得到 $K \times 4 \times 1$ 的结果. #### 多尺度时序模式特征重标定 将上一部分的特征模式看作局部感受野在空间和特征维度的信息聚合. 使用SENet对信息进行重标定. ##### 实现 > SENet的思想是: > 通过网络根据Loss去学习特征权重, 使得有效的feature map权重大, 无效或效果小的feature map权重小的方式是训练达到更好的效果. 将上一步分得到 $K \times 4 \times 1$ 的特征称为 $U$. SENet分为2个步骤: Squeeze 和 Excitation. 首先对 $U$ 进行 Gloval Average Pooling, 得到一个 $K \times 1 \times 1$ 的数据(Squeeze), 紧接着对这个数据进行两次Fully Connect(Excitation), 最后使用Sigmoid(激活函数)将权值限定在 $[0,1]$ 中, 得到Scale-$C$ ($K \times 1 \times 1$). 最后, 将得到的 $C$ 的每个Scale值 乘到 $U$ 对应的每一层中, 得到该模块的输出. 简而言之, 通过控制scale大小, 把重要的数据增强, 而不重要的数据则减弱. ## 实验数据与结果分析 ### 数据 作者采用三个公开数据集: - Canteen-Dining: 高校2019年春季学期某校区全校师生的校园一卡通消费数据,以每30分钟为时间间隔统计全校师生在21 个食堂的人流量记录. - Canteen-Consumption: 高校2019年春季学期某校区21个食堂的流水记录, 即各个食堂每间隔半小时的消费总金额. - Solar-Energy: Alabama州级2006年太阳能生产记录,包含137个光伏发电厂每间隔10分钟读取的太阳能发电数据. 其中前2个数据集, 将前12个教学周为训练集, 中间4个教学周为验证集, 后4个教学周为测试集. 最后一个数据集前219天作为训练集, 中间73天作为验证集, 后73天作为测试集. 对这三个数据集计算一个时序信号 $\boldsymbol{X}_t$ 与自身在不同时刻的互相关程度: $$ R(\tau) = \frac{E[(\boldsymbol{X}_t-\mu)(\boldsymbol{X}_{t+\tau}-\mu)]}{\sigma^2} $$ $\mu$, $\sigma$ 分别表示时序信号 $\boldsymbol{X}_t$ 的均值和标准差. 可以发现数据集都是存在较高的自相关性的重复模式. ### 结果分析 作者将MSCNN与7种时序预测方法进行比较:  通过采用 RSE, CORR, 预测准确率(Accuracy@E) 三种度量方式来评估预测性能. 根据实验得到的RSE和CORR在多数情况下是优于其他模型的.  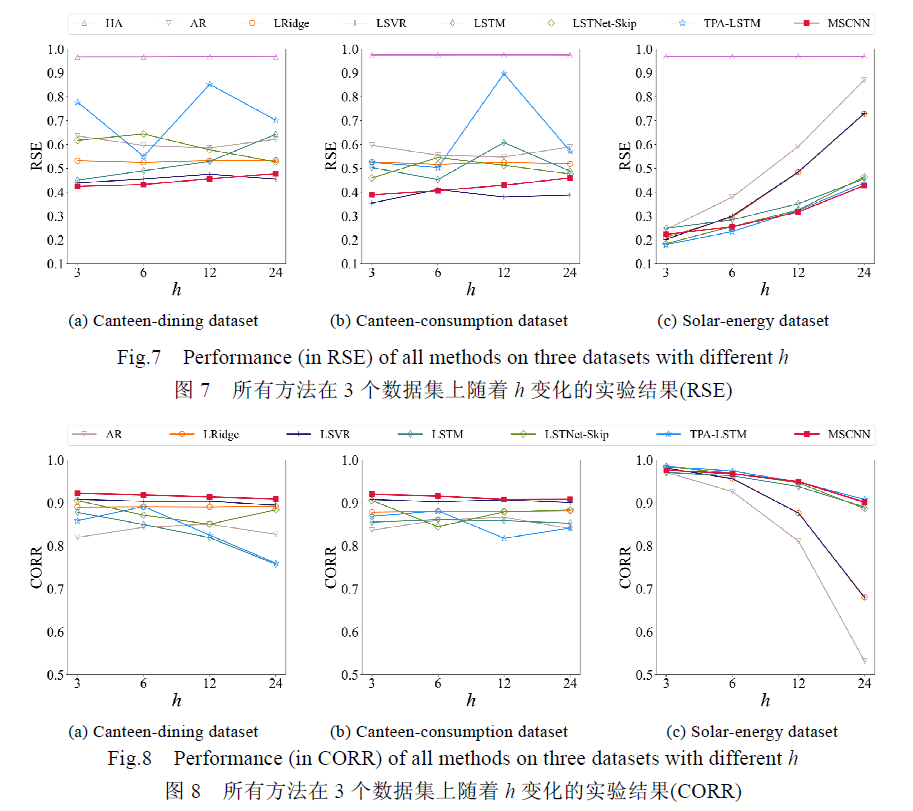 在 $h=3$ 的Accuracy@E指标, MSCNN在4个指标中取得了最优的成果.  ## 总结 MSCNN 利用短时以来, 长时周期模式和变量相互依赖特征, 以及融合组件对特征进行重标定, 在准确率和运行速度上都要优于目前的其他模型. 预测校园人流量目前仅仅是依据区域与区域, 时间与时间之间的关系在进行预测的, 而通常情况下, 人流量也受其余因素的影响, 例如: 考试周, 节假日等等. 通过可以通过其余考量对模型进行进一步的优化, 提升模型的准确度. 最后修改:2021 年 08 月 28 日 © 允许规范转载 赞 0 如果觉得我的文章对你有用,请随意赞赏