Loading... # Chapter.2 机器学习攻略 > PDF: [https://mki.moe/usr/uploads/2021/07/1202451733.pdf](/usr/uploads/2021/07/1202451733.pdf) ## 当模型loss较大的时候, 如何进行调整 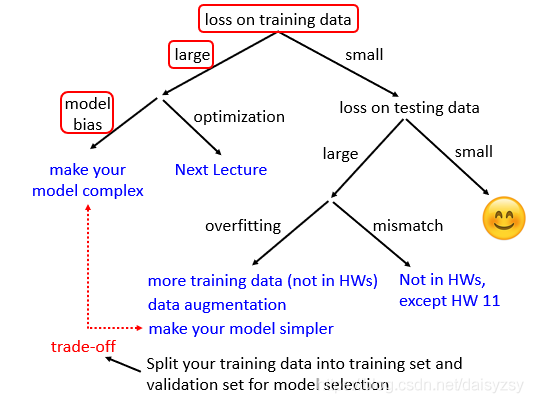 ### 1. Model bias - 模型本身带来的偏差 模型过于简单, 无法找到某一个假设使得模型很好的拟合训练数据, 这个时候应当增加模型的复杂性, 让模型更复杂一些 解决办法: - 添加更多的特征 - 添加更多的网络层 - 选择一个更复杂的model ### 2. Optimization Issue - 模型没有调优至最佳 训练过程中模型陷入局部最优, 在现有的假设空间内算法调优不仅没有找到最优解 > *区分是 `Model bias` 还是 `Optimization Issue`* > > 在现有模型上先增加模型的复杂度, 比如多一些层, 然后看看加了模型复杂度之后, 模型在训练集上的training loss是不是有所下降. 若下降了则是 `Model bias`, 上升了则是 `Optimization Issue` ### 3. Overfitting 解决方法: - 增加训练数据, 数据增强 - 给与模型一些限制, 缩小假设空间 ### 4. Mismatch 训练集的数据分布和测试集的数据分布不一样导致 解决办法: - 实际过程中遇到这种情况,调整训练集和测试集即可 --- ## Saddle point & Local Minima ### Optimization失败的原因 Gradient为0时, 当前可能位于`Critical Point (驻点)`, 在 `Critical Point` 可能存在两种可能: - `Local Minima`: 局部最小点 - `Saddle Point`: 鞍点 ### 判断当前位于 Local Minima 还是 Saddle Point > 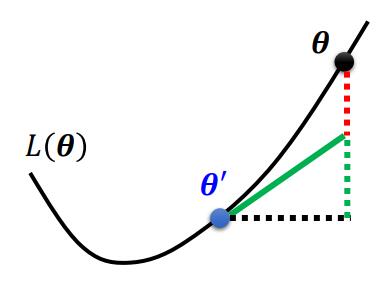 $L(\theta)$ 在 $\theta = \theta'$ 附近的图像近似于 $$ L(\theta) \approx L(\theta') + (\theta-\theta')^T g + \frac{1}{2}(\theta-\theta')^T H (\theta-\theta') $$ 其中, - $g$ 为 Gradient Vector (梯度向量) - $g= \nabla L(\theta)$, $g_i=\frac{\partial L(\theta')}{\partial \theta_i}$ - $H$ 为 Hessian Matrix (海瑟矩阵) - $H_{ij} = \frac{\partial^2}{\partial \theta_i \partial \theta_j}L(\theta')$ 当处于 Critical Point 时, $$ L(\theta) \approx L(\theta')+\frac{1}{2}(\theta - \theta')^T(\theta-\theta') $$ 设 $$ v=(\theta - \theta') $$ 此时, $$ L(\theta) \approx L(\theta') + \frac{1}{2} v^T H v $$ > 通过分析 $v^T H v$, 可以得到当前 Critical Point 的情况: > > 1. 对于所有 $v$, 当 $v^T H v > 0$ 时, $L(\theta) > L(\theta')$, 则此时 Critical Point 处于 Local Minima; > 2. 对于所有 $v$, 当 $v^T H v < 0$ 时, $L(\theta) < L(\theta')$, 则此时 Critical Point 处于 Local Maxima; > 3. 当存在部分 $v$, 使 $L(\theta) > L(\theta')$, 又存在另一部分 $v$, 使 $L(\theta) < L(\theta')$, 则此时 Critical Point 处于 Saddle Point. 换言之, 1. 当 $H$ 正定时(所有特征值为正), 则当前 Critical Point 位于 Local Minima; 2. 当 $H$ 负定时(所有特征值为负), 则当前 Critical Point 位于 Local Maxima; 3. 当 $H$ 即存在正的特征值, 又存在负的特征值, 则当前 Critical Point 位于 Saddle Point. ### 逃离 Saddle Point 的方法 当 Critical Point 位于 Saddle Point 时, $H$ 会告诉参数此时变更的方向. 设 $u$ 为 $H$ 的特征向量, $\lambda$ 为特征向量 $u$ 的特征值, 此时: $$ u^T H u = u^T(\lambda u) = \lambda \lVert u \rVert^2 $$ 当 $\lambda < 0$ 时, $u^T H u = \lambda \lVert u \rVert ^2 < 0$, 此时 $$ L(\theta) \approx L(\theta')+\frac{1}{2}(\theta - \theta')^TH(\theta - \theta') $$ 令 $u = \theta - \theta'$, 得到 $$ L(\theta) < L(\theta') $$ > 因为 $u = \theta - \theta'$, 则 $\theta = \theta' + u$, $L$ 减小 ### Example 定义: - 模型: $y = w_1 w_2 x$; - 训练集: $D(x,\hat{y})=\{(1,1)\}$ - 定义损失函数: $L=(\hat{y}-w_1 w_2 x)^2$ 根据训练集, 损失函数可简化为: $L=(\hat{y}-w_1 w_2 x)^2 = (1-w_1w_2)^2$ 计算微分: $$ \frac{\partial L}{\partial w_1} = 2(1-w_1w_2)(-w_2) = 0 $$ $$ \frac{\partial L}{\partial w_2} = 2(1-w_1w_2)(-w_1) = 0 $$ $$ \frac{\partial^2 L}{\partial w_1^2} = 2(-w_2)(-w_2) = 0 $$ $$ \frac{\partial^2 L}{\partial w_1w_2} = -2+4w_1w_2 = -2 $$ $$ \frac{\partial^2 L}{\partial w_2w_1} = -2+4w_1w_2 = -2 $$ $$ \frac{\partial^2 L}{\partial w_2^2} = 2(-w_1)(-w_1) = 0 $$ 综上, - Critical Point: $(w_1, w_2) = (0,0)$ - Gradient Vector: $g=\begin{bmatrix}w_1 \\ w_2 \end{bmatrix}=\begin{bmatrix}0 \\ 0 \end{bmatrix}$ - Hessian Mattix: $H = \begin{bmatrix}0 & -2 \\ -2 & 0 \end{bmatrix}$ - Eigen Value: $\lambda_1 = 2, \lambda_2 = -2$ 根据Eigen Value $\lambda_1$, $\lambda_2$, 可得当前Critical Point $(0,0)$ 位于 Saddle Point 此时, $\lambda_1 = 2$, $u=\begin{bmatrix} 1 \\ 1 \end{bmatrix}$, 此时朝着 $u$ 的方向进行变换, 即可逃离 Saddle Point > 在实际操作中, 很少使用此方法用来逃脱 Saddle Point. 因为计算二阶导对算力压力十分大. --- ## Batch And Momentum ### 较小的 Batch Size 与较大的 Batch Size比较 | item | Small Batch Size | Large batch Size | | :---: | :----: | :----: | | Update速度 (非并行) | 快 | 慢 | | 1 epoch 时间 | 相同 | 相同 | | Gradient | 噪声较大 | 稳定 | | Optimization (优化) | 更好 | 略差 | | Optimization (泛化性) | 更好 | 略差 | ### Momentum > - Gradient Descent: 往计算值的反方向进行更新 > - Gradient Descent With Momentum: Gradient Descent 的反方向 + 前一步移动的方向 > > 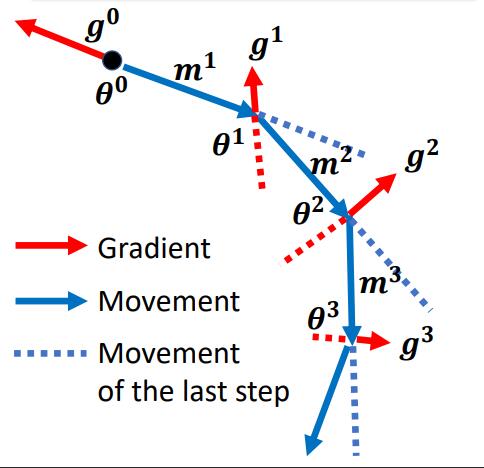 #### 步骤 1. 在 $\theta^0$ 处开始 2. 移动距离 $m^0 = 0$ 3. 计算梯度 $g^0$ 4. 计算移动距离 $m^1=\lambda m^0 - \eta g^0$ 5. 移动 $\theta^1 = \theta^0 + m^1$ 6. 计算梯度 $g^1$ 7. 计算移动距离 $m^2=\lambda m^1 - \eta g^1$ --- ## Learning Rate (学习速率) 从梯度下降公式 $\theta \to \theta + \eta g$ 可以发现, 存在一个参数学习速率 $\eta$, 假如模型训练至某一时刻, 发现 training loss 不再下降, 并不一定是陷入了 Local Minima 或者 Saddle Point. 还有一种可能是因为此时的学习率 $\eta$ 已经很小了. 实际上, 让一个 model 陷入 Local Minima 是很难的, 让 Gradient 为 0 通常不会发生, 例如: - 当 $\eta$ 很大时, 梯度更新会十分震荡, 几乎走不到最优点; - 当 $\eta$ 很小时, 难以收敛至最优点. 如 `Pic 2-3`. 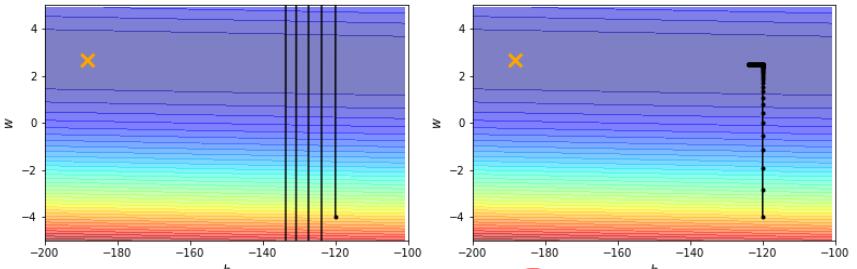 ### 自动学习速率 > 该节部分内容借鉴自: https://zhuanlan.zhihu.com/p/355091448 为了解决上述的问题, 可以通过自动学习速率解决. 当前方向的梯度比较大的时候, 设置较小的学习率; 而当前梯度较小的时候, 设置较大的学习率. 当需要更新第 $i$ 个参数 $\theta_i$ 在 $t+1$ 时刻的 Gradient Descent: $$ \theta^{t+1}_i \leftarrow \theta^{t}_i - \eta g_i^t $$ $$ g^t_i=\frac{\partial L}{\partial \theta_i}\bigg |_\theta=\theta^t $$ 使用定制化的 Gradient Descent, 给每个 $t$ 时刻 $\theta_i$ 的学习速率 $\eta$ 设定一个系数 $\sigma^t_i$: $$ \theta^{t+1}_i \leftarrow \theta^t_i - \frac{\eta}{\sigma^t_i} g^t_i $$ #### 自动学习速率的优化算法 ##### 1. Root Mean Square $$ \sigma^t_i = \sqrt{\frac{1}{t+1} \sum^t_{i=0}(g^t_i)^2} $$ 依据参数 $\theta_i$ 在当前时刻学习率系数 $\sigma^t_i$ 和过去的梯度 $g$ 的平方和有关. `RMS` 通常用于 `Adagrad` 算法 ##### 2. RMSProp $$ \sigma^t_i = \sqrt{\alpha(\sigma^{t-1}_i)^2+(1-\alpha)(g^t_i)^2},\ \sigma^0_i = \sqrt{(g_i^0)^2} = \lvert g^0_i \rvert,\ 0 < \alpha < 1 $$ `Adagrad` 算法通常用于较为平缓的曲线, 而实际运用中, Local Minima 通常同时存在陡峭和平缓的部分. 我们需要学习率可以自适应当前曲线的陡峭程度: - 曲线平滑的地方, 学习率设置较大; - 曲线陡峭的地方, 学习率设置较小. `RMSProp` 中, 假如当前走到了一个比较陡的坡度, 我们会希望当前的 gradient $g$ 尽量小, 此时 $\alpha$ 较大; 反之相反. ##### 3. Adam 被认为是 RMSProp 与 Momentum 的结合, 其中: - Momentum 是对Gradient $g$ 本身的改进优化; - RMSProp 是自适应的调整学习率, 使模型能够快速并且稳定的到达最优点. ##### 4. Learning Rate Decay 当给定了学习速率 $eta$ 时, 随着 $t$ 的不断增大, $\sigma$ 会不断减少, 此时 $\frac{\eta}{\sigma}$ 反而会不断增大. 因此, 为了曲线收敛的更平稳, 需要对 $\eta$ 做限制. 随着训练的进行, 当我们越接近目标点时, 需要逐渐减小 $\eta$ 的值. ##### 5. Warm Up > `Warm Up`策略具体内容可参考 [论文](https://arxiv.org/abs/1908.03265) 和 [Zhihu](https://www.zhihu.com/question/338066667) `Learning Rate Decay` 中的 $\eta$ 时不断衰减的, 而 `Warm Up` 的策略时先让 $eta$ 增大, 随后在逐步减少. #### 总结 上面所有方法都可以用一个式子做总结: $$ \theta^{t+1}_i \leftarrow \theta^t_i - \frac{\eta}{\sigma^t_i} g^t_i $$ 根据公式我们可以得到, 更新对象就是 $\sigma$, $\eta$, 以及当前的梯度 $g$. 其中 `Root Mean Square`, `RMSProp`, `Adam` 是通过对 $\sigma$ 进行改进的方法; 而 `Learning Rate Decay`, `Warm Up` 则是对 $\eta$ 本身进行改进. --- ## Classification 通常 `Regression` 的步骤: $$ x \to \boxed{\text{MODEL}} \to y \leftarrow \cdots \rightarrow \hat{y} $$ 我们可以类似的方法进行 `Classification`: $$ x \to \boxed{\text{MODEL}} \to y \leftarrow \cdots \rightarrow \hat{y}\text{(class)} $$ 对于`Classification` 问题, 输出的结果 $\hat{y}$ 可以使用 `One-hot vector` 来表示, 如: $$ \hat{y} = \begin{bmatrix}1 \\ 0 \\ 0 \end{bmatrix} \text{or} \begin{bmatrix}0 \\ 1 \\ 0 \end{bmatrix} \text{or} \begin{bmatrix}0 \\ 0 \\ 1 \end{bmatrix} $$ 来分别表示 Class1, Class2, Class3. 对于 `Regression` 的模型, 用矩阵形式表示: $$ \hat{y} \leftarrow \cdots \rightarrow y=b+c^T\sigma (b+Wx) $$ 而对于 `Classification` 的模型, 用矩阵形式表示: $$ y=b'+W'\sigma (b+Wx) $$ 通常会对模型输出 $y$ 进行 `softmax` 操作得到 $y'$, 再于 `Label` $\hat{y}$ 比较 $$ \hat{y} \leftarrow \cdots \rightarrow y' = \text{softmax}(y) $$ 其中, - $\hat{y}$ 为 $0$ 或 $1$ - `Soft-max` 的作用是将预测值 $y$ 移动至 $0-1$ 之间, 做 `normalization` - $y$ 可以是任意值 ### Soft-max `Soft-max` 的作用是将预测值 $y$ 移动至 $0-1$ 之间, 做 `normalization`. $$ y_i'=\frac{\exp(y_i)}{\sum_j \exp (y_i)}, (0<y_i'<1, \sum_i y_i = 1) $$ 一般只有两个分类时, 可以取用 `sigmoid`; 而多个时则使用 `Soft-max`. (实际上是相同的) ### Loss of Classification 定义: $L = \frac{1}{N} \sum_n e_n$ 过程: $$ \hat{y} \leftarrow \cdots \rightarrow y' \leftarrow \boxed{\text{SOFTMAX}} \leftarrow y \leftarrow \boxed{\text{NETWORK}} \leftarrow x $$ 有多种方法计算Loss, 通常使用 `Cross-entropy (交叉熵)`: $$ e = -\sum_i \hat{y_i}\ln y_i' $$ > 最小交叉熵等价于最大似然 --- ## Batch Normalization > 该段内容主要来自: https://samaelchen.github.io/deep_learning_step5/ `Normalization` 是以前统计学习比较常用的一种方法, 因为对于损失函数而言, $L(\hat{y},y)$ 会受到输入数据的影响. > 比如说一个数据有两个维度, 一个维度都是 $1-10$ 的范围内波动的, 另一个维度是 $1000-10000$ 之间波动的. 那么如果 $y=x_1+x_2$ 很明显后一个维度的数据对 $y$ 的影响非常大. 那么此时做 Gradient Descent, 在 Scale 大的维度上梯度就比较大, 但是在 Scale 小的地方梯度就比较小, 如`Pic 2-4` 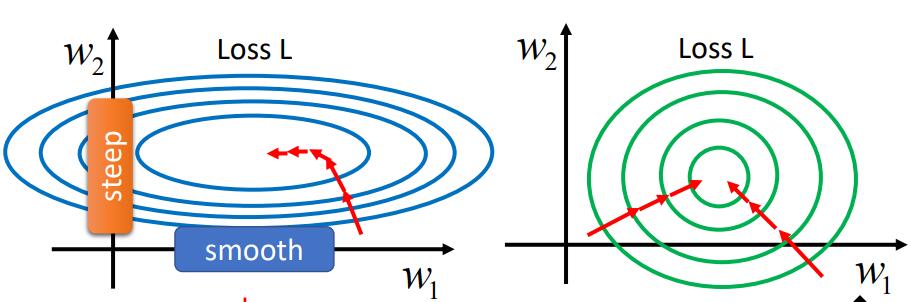 那这样在不同维度上的梯度下降步长是不一样的. 所以在统计学习或者传统的机器学习里面, 为了加快收敛的速度, 虽然用二阶导可以解决, 但是一般用 `Feature Scaling` 就可以了. 而 `Batch Normalization` 其实也是使用了这样的理念. 一般而言, 我们做 `Normalization` 就是 $\frac{x-\mu}{\sigma}$, 那 `Batch Normalization` 其实就是在每一个 layer 的输入前做这么一下操作. 我们平常在进行训练时, 会分 Batch 导入数据, 这种情况我们无法得到全局的 $\mu$ 和 $\sigma$. `Batch Normalization` 与 `Normalization` 的区别, 就是 `Batch Normalization` 计算的时每一个 Batch 的 $\mu$ 和 $\sigma$. 如果说觉得这样全部 `Normalization` 到 $0$, $1$ 这样的形式可能有些 `Activation Function` 效果不好, 所以我们可以考虑一下再加一层 `Linear Layer` 来转换一下. 两个流程总结如 Pic 2-5: 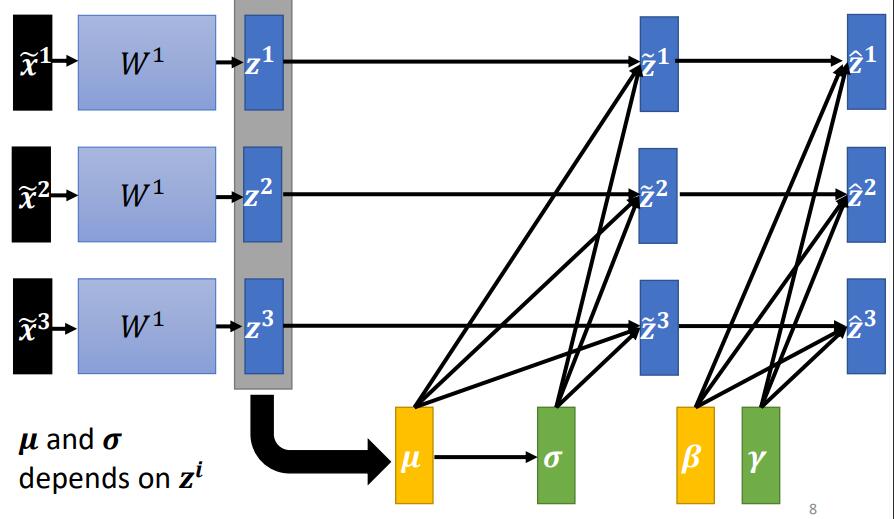 ### Testing of Batch Normailzation 在训练过程中, 我们一般都是分批次的 Batch 喂进去, 但是 Test 的时候一般是一次性把数据过一遍, 那么我们并没有办法得到一个合适的 $\mu$ 和 $\sigma$. 解决方法是计算一下全部数据集 $D$ 的均值和标准差. 另一种方法是, 每次训练后, 我们都保留最后一个 Batch 的均值和标准差 (Moving Average), 过程如下 $$ \tilde{x} \to \boxed{W'} \to z \stackrel{\tilde{z} = \frac{z-\bar{\mu}}{\bar{\sigma}}} \to \tilde{z} \to \cdots $$ $$ \bar{\mu} \leftarrow p\bar{\mu} + (1-p)\mu^t $$ --- 该笔记的部分内容主要借鉴以下几篇博客(已在文中进行标注): 1. 自动学习速率 - https://samaelchen.github.io/deep_learning_step5 2. Batch Normalization - https://zhuanlan.zhihu.com/p/355091448 最后修改:2021 年 07 月 28 日 © 允许规范转载 赞 0 如果觉得我的文章对你有用,请随意赞赏