Loading... # Chapter 1 HW > PDF: [https://mki.moe/usr/uploads/2021/07/3961049197.pdf](/usr/uploads/2021/07/3961049197.pdf) ## HW 1-1 > 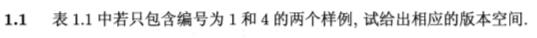 样例如下: | 编号 | 色泽 | 根蒂 | 敲声 | 好瓜 | | :---: | :---: | :---: | :---: | :---: | | 1 | 青绿 | 蜷缩 | 浊响 | 是 | | 4 | 乌黑 | 稍蜷 | 沉闷 | 否 | ### Solve 可以先得到样本空间, 共 $(2+1)*(2+1)*(2+1)+1=28$ 种: | # | 色泽 | 根蒂 | 敲声 | | :---: | :---: | :---: | :---: | | 1 | 青绿 | 蜷缩 | 浊响 | | 2 | 青绿 | 蜷缩 | 沉闷 | | 3 | 青绿 | 蜷缩 | * | | 4 | 青绿 | 稍蜷 | 浊响 | | 5 | 青绿 | 稍蜷 | 沉闷 | | 6 | 青绿 | 稍蜷 | * | | 7 | 青绿 | * | 浊响 | | 8 | 青绿 | * | 沉闷 | | 9 | 青绿 | * | * | | 10 | 乌黑 | 蜷缩 | 浊响 | | 11 | 乌黑 | 蜷缩 | 沉闷 | | 12 | 乌黑 | 蜷缩 | * | | 13 | 乌黑 | 稍蜷 | 浊响 | | 14 | 乌黑 | 稍蜷 | 沉闷 | | 15 | 乌黑 | 稍蜷 | * | | 16 | 乌黑 | * | 浊响 | | 17 | 乌黑 | * | 沉闷 | | 18 | 乌黑 | * | * | | 19 | * | 蜷缩 | 浊响 | | 20 | * | 蜷缩 | 沉闷 | | 21 | * | 蜷缩 | * | | 22 | * | 稍蜷 | 浊响 | | 23 | * | 稍蜷 | 沉闷 | | 24 | * | 稍蜷 | * | | 25 | * | * | 浊响 | | 26 | * | * | 沉闷 | | 27 | * | * | * | | 28 | $\varnothing$ | $\varnothing$ | $\varnothing$ | 然后根据样本, 一条条删除与正例不符的样本, 得到剩下的即为版本空间: | # | 色泽 | 根蒂 | 敲声 | | :---: | :---: | :---: | :---: | | 1 | 青绿 | 蜷缩 | 浊响 | | 3 | 青绿 | 蜷缩 | * | | 7 | 青绿 | * | 浊响 | | 9 | 青绿 | * | * | | 19 | * | 蜷缩 | 浊响 | | 21 | * | 蜷缩 | * | | 25 | * | * | 浊响 | ## HW 1-2 >  样例如下: ### Solve 根据样例, 共有3个属性 - `色泽`, `根蒂`, `敲声`: `色泽` 有 2 个种类, `根蒂`有 3 个种类, `敲声`有 3 个种类. 又因为存在正例, 排除 $\varnothing$ 的假设. 我们可以计算单个合取式的假设空间规模: $(2+1)*(3+1)*(3+1)=48$. 接下来做的事就是将 $48$ 个合取式挑 $i (i \leq k)$ 种进行组合, 我们可以简单的得到此时所有可能的假设数量 $N$: $$ N = \sum_{i=1}^k C^i_k $$ 我们注意到因为存在题目提示冗余情况, 根据逻辑等价式的分配率[^1]: $$ (A \land B) \lor (A \land C) \equiv A \land (B \lor C) $$ 因此存在通配符(``*``)时, 可能出现以下可能: $$ \begin{aligned} \Big( (x_1=a) \land (x_2=b) \Big) \lor \Big((x_1=a) \land (x_2=*)\Big) & \Leftrightarrow (x_1=a) \land \Big( (x_2=b) \lor (x_2=*) \Big) \\ & \Leftrightarrow (x_1=a) \land (x_2=*) \end{aligned} $$ 我们注意到题目中 $k$ 使用了修饰词 <mark>最多</mark>. 根据上述冗余情况将其合并, 得到结论: 在假设空间中, 每个析合范式未必具有同样个数的合取式. 因此 $k$ 为假设空间中析合范式中所含合取式个数的最大值并非为 $48$. 不难发现, 当一个析合范式包含了所有不含泛化通配符 ``*`` 的 $2*3*3=18$ 个合取式时, 若再添加包含泛化通配符 ``*`` 的合取式, 则必然会造成冗余, 合取式必然会被消除而减少. 因此我们可以得到 $k_{max} = 18$. 故得到答案, $k=k_{max}=18$ 时, 共有可能的假设数量 $N$: $$ N = \sum_i^k C^i_k = \sum_i^{18} C^i_{18} = 2^{18} = 262143 $$ ## HW 1-3 >  ### Solve 直接想法是存在噪声就尽可能地消除噪声. - 若存在两个样例属性取值都相同, 标记却不同, 则只保留标记为正例(或反例)的样例; 除此之外, 另外, 考虑归纳偏好应尽量与问题相匹配, 这里可使归纳偏好与噪声分布相匹配. ## HW 1-4 >  $$ E_{ote}(\mathcal{L}_a|X,f) = \sum_h \sum_{x \in \mathcal{X}-X} P(x)\ l(h(x), f(x))\ P(h|X,\mathcal{L}_a) \tag{1.3} $$ ### Solve 类似于笔记 *式1.2* 的计算. 假设 $f$ 是均匀分布的, 一半的 $f$ 对 $\boldsymbol{x}$ 的预测与 $h(\boldsymbol{x})$ 不一致, 另一半则一致. 根据 *式1.3*, 得到: $$ \sum_f E_{ote}(\mathcal{L}_a|X,f) = \sum_f \sum_h \sum_{x \in \mathcal{X}-X} P(x)\ l(h(\boldsymbol{x}), f(\boldsymbol{x}))\ P(h|X,\mathcal{L}_a) \tag{1.4} $$ 计算 *式1.4*: $$ \begin{aligned} \sum_f E_{ote}(\mathcal{L}_a|X,f) &= \sum_f \sum_h \sum_{x \in \mathcal{X}-X} P(x)\ l(h(\boldsymbol{x}), f(\boldsymbol{x}))\ P(h|X,\mathcal{L}_a) \\ &= \sum_{\boldsymbol{x} \in \mathcal{X}-X} P(\boldsymbol{x}) \sum_h P(h|X,\mathcal{L}_a) \sum_f l(h(\boldsymbol{x}), f(\boldsymbol{x})) \\ \end{aligned} $$ 由于 $f$ 均匀分布, 一半的 $f$ 对 $\boldsymbol{x}$ 的预测与 $h(\boldsymbol{x})$ 不一致. 同时对于二分类问题, 预测成功(失败)的度量分数应当如同 *式1.2* 中的 $\mathbb{I}(\cdot)$, 是固定且一致的. 那么此时我们可以设函数 $l(h(\boldsymbol{x}),f(\boldsymbol{x}))$ 中: - $h(\boldsymbol{x}) = f(\boldsymbol{x})$ 时, $l=A_1$ - $h(\boldsymbol{x}) \neq f(\boldsymbol{x})$ 时, $l=A_2$ 得到: $$ \begin{aligned} \sum_f l(h(\boldsymbol{x}), f(\boldsymbol{x})) &= \frac{1}{2} \cdot 2^{|\mathcal{X}|} \cdot A_1 + \frac{1}{2} \cdot 2^{|\mathcal{X}|} \cdot A_2 \\ &= \frac{1}{2} \cdot 2^{|\mathcal{X}|} \cdot (A_1+A_2) \\ &= \frac{1}{2} A\cdot 2^{|\mathcal{X}|} \end{aligned} $$ 将上式代入并继续计算: $$ \begin{aligned} \sum_f E_{ote}(\mathcal{L}_a|X,f) &= \sum_f \sum_h \sum_{x \in \mathcal{X}-X} P(x)\ l(h(\boldsymbol{x}), f(\boldsymbol{x}))\ P(h|X,\mathcal{L}_a) \\ &= \sum_{\boldsymbol{x} \in \mathcal{X}-X} P(\boldsymbol{x}) \sum_h P(h|X,\mathcal{L}_a) \sum_f l(h(\boldsymbol{x}), f(\boldsymbol{x})) \\ &= \frac{1}{2} A\cdot 2^{|\mathcal{X}|} \sum_{\boldsymbol{x} \in \mathcal{X}-X} P(\boldsymbol{x}) \sum_h P(h|X,\mathcal{L}_a) \\ &= 2^{|\mathcal{X}|-1} A \sum_{\boldsymbol{x} \in \mathcal{X}-X} P(\boldsymbol{x}) \cdot 1 \\ &= 2^{|\mathcal{X}|-1} A \sum_{\boldsymbol{x} \in \mathcal{X}-X} P(\boldsymbol{x}) \end{aligned} $$ 得到了与 *式1.2* 类似的结论, 度量结果与学习算法 $\mathcal{L}$ 无关, NFL仍成立. ## HW 1-5 >  ### Solve 1. 在向搜索引擎提交信息的阶段, 能够从提交文本中进行信息提取, 进行语义分析; 2. 在搜索引擎进行信息匹配的阶段, 能够提高问题与各个信息的匹配程度; 3. 在向用户展示搜索结果的阶段, 能够根据用户对结果感兴趣的程度进行排序. [^1]: *《离散数学及其应用》* P.25 最后修改:2021 年 07 月 29 日 © 允许规范转载 赞 0 如果觉得我的文章对你有用,请随意赞赏