Robustra: Training Provable Robust Neural Networks over Reference Adversarial Space

博主： ShaneG_Miku
发布时间：2022 年 04 月 05 日
963 次浏览
暂无评论
5931字数
分类：论文笔记

## Abstract

目前机器学习, 尤其是深度神经网络(DNN)被广泛应用于多个领域, 如图像识别、语音识别等. 然而有研究表示, DNN模型通常极易被精心设计的对抗性攻击所误导, 比如对抗性样例(adversarial example): 攻击者通过在输入样例上添加一个难以发现的扰动, 以此欺骗神经网络输出错误的结果, 对抗性攻击的存在给基于DNN的应用带来了极大的安全问题.

文章提出了一种基于 **Linear Dual** 和 **Transferability-based trainging** 的方法 *Robustra*[^2]. 首先, Robustra对ReLU函数的松弛, 通过利用引用模型的对抗空间来作为可行域, 来解决攻击与防御两者之间的Min-Max问题; 接着, 将Min-Max问题转化为对应的对偶问题, 通过线性逼近攻击者的最佳策略和参考模型引入的松弛变量单调性来解决这个对偶问题, 其对偶问题的解即对应原Min-Max问题的解.

## Introduction

DNN目前虽然被广泛应用, 但是通常DNN很容易被一些恶意的扰动所干扰. 这些干扰虽然无法被肉眼所察觉, 但是能够很轻松的欺骗DNN. 这阻扰了DNN模型在安全敏感领域的应用: 如自动驾驶和控制系统.

以视觉深度神经网络(Vision-based DNN)为例, 如下图: 经过训练后我们得到一个DNN, 此时我们输入一个原始图像 $x$, 模型能够正常输出标签 `dog`; 然而攻击者通过设计一个扰动 $\Delta x$, 并将扰动叠加至原图像上得到了一个对抗性样例 $x'=x+\Delta x$, 此时, 模型无法正确预测该对抗性样例为 `dog`, 而是 `Struthio camelus`.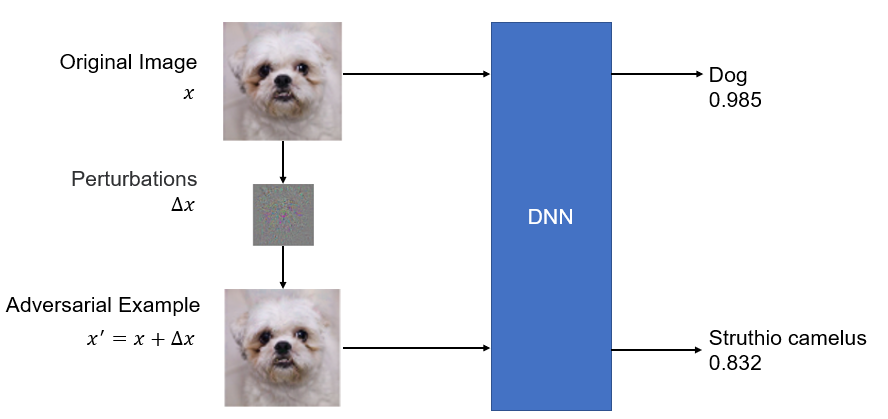

![Adversarial Example of Vision-based DNN](/usr/uploads/2022/04/3663001837.png)

因此, 对于上述的例子, 可以定义: 对于输入样本 $x$ 范式球内的所有 $x'$, 若模型对这两者都能输出相同的标签, 则 Vision-based DNN 是具有鲁棒的:

$$
\forall x':\Vert x-x'\Vert_p \leq \delta \to f(x)=f(x')
$$

目前已有多种方法对神经网络进行鲁棒性验证或鲁棒性训练, 目前验证有两种主要的方法: 确定性方法验证和概率方法验证. 其中确定性方法又可分为完全验证和不完全验证. 本文使用了一种基于 **Linear Dual** 和 **Transferability-based trainging** 的方法:

- Linear Dual 是对ReLU进行松弛的一种方法, 其核心是将鲁棒性验证看作是一个优化问题. 首先对ReLU函数进行松弛, 将高度非凸的问题转化为一个线性规划问题, 接着通过将原问题转化为对偶问题的方法, 得到原问题最优解.
- Transferability-based trainging 通过鲁棒训练的方法去训练神经网络, 是神经网络拥有更好的鲁棒性. 这种方法通过引用一个一训练的模型训练一个新的模型, 又或是互相引用训练, 以提高模型的准确性.

## Method

### 问题定义

首先定义一个基于ReLU激活函数的神经网络 $f$, $g$:

$$
\begin{cases}
z_0 = x \in \mathbb{R}^n \\
z_i=\text{ReLU}(W_i z_{i-1} + b_i), 1 \leq i \leq k_1 \\
f(x) = z_{k_1} \in \mathbb{R}^m
\end{cases}
$$

$$
\begin{cases}
w_0 = x \in \mathbb{R}^n \\
w_i=\text{ReLU}(U_i w_{i-1} + d_i), 1 \leq i \leq k_2 \\
g(x) = w_{k_2} \in \mathbb{R}^m
\end{cases}
$$

其中, $f$ 为等待训练的模型, $g$ 引用模型. $\theta$ 为模型 $f$ 中需要训练的参数

给定一个样本: $x^\ast$; 样本标签: $y^\ast$; 目标标签: $y^\text{targ}, y^\text{targ} \neq y^\ast$, 我们可以得到模型 $g$ 在 $l_\infty$ 范数约束下的对抗样本空间:

$$
\mathcal{A}_\epsilon(x^\ast) = \Big\{x:
\big(\Vert x-x^\ast \Vert_\infty \leq \epsilon \big) 
\land 
\Big( \big(g(x)\big)_{y^\text{targ}} - \big(g(x)\big)_{y^\ast} \geq t \Big)
\Big\}
$$

对于上式, 其中 $t$ 为对抗性样例和决策边界之间的距离:

- $t = 0$ 时, 即模型 $g$ 输出实际标签概率与样本标签概率相同时, $\mathcal{A}_\epsilon(x^\ast)$ 正好为 $g$ 的对抗空间
- $t$ 减小时, 即模型 $g$ 输出样本标签概率不断增大时, 对抗空间变大; 反之相反.

我们的目标是希望从 $g$ 的对抗空间 $\mathcal{A}_\epsilon(x^\ast)$ 的样本训练模型 $f$ , 使模型 $f$ 能够抵御引用模型 $g$ 的对抗样例, 即:

$$
\forall y^\text{targ}, \min_\theta \Big( \max_x \big( f_\theta(x) \big)_{y^\text{targ}} - \big( f_\theta(x) \big)_{y^\ast} \Big), \\
\text{s.t. } x \in \mathcal{A}_\epsilon(x^\ast)
$$

令 $c=e_{y^\text{targ}} - e_{y^\ast}$, $\mathcal{F}_\mathcal{A}(x^\ast)=\{ f_\theta(x): x \in \mathcal{A}_\epsilon(x^\ast)\}$, 上式可以等价改写为:

$$
\forall y^\text{targ}, \min_\theta \max_v c^\top v, \\
\text{s.t. } v \in \mathcal{F}_\mathcal{A}(x^\ast)
$$

接下来, 训练模型 $f$ 的主要问题就是如何求解上式这个优化问题.

### ReLU松弛

根据问题定义, 我们可以知道由于神经网络的激活函数是非线性的, 因此该优化问题是高度非凸的, 因此解决上述的Min-Max问题十分困难. 因此, 文章使用了ReLU松弛的办法, 如下图.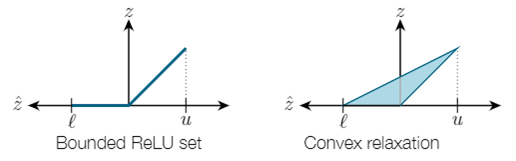

![ReLU Relaxation](/usr/uploads/2022/04/1348255019.png)

文章将ReLU函数 $y=\max\{x, 0\}$ , 如上图, 通过松弛:

$$
\begin{cases}
o=0, &l\leq u \leq 0 \\
o=i, &0 \leq l \leq u \\
(u-l) o \leq u(i-l) \land o \geq 0. &i\leq i
\end{cases}
$$

通过松弛将非线性的ReLU函数通过线性进行约束, 如下图, 文章先对引用模型 $g$ 中的每个ReLU函数进行松弛, 再类似的对训练模型 $f$ 中的每个ReLU 进行松弛.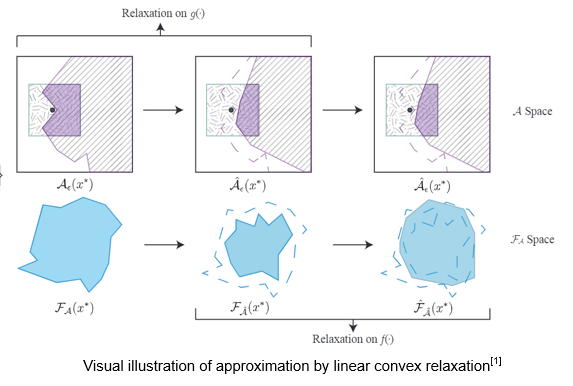

![](/usr/uploads/2022/04/3940231651.png)

根据上图可以发现, 原非凸的问题经过松弛后, 变成了一个凸问题, 此时, 我们可以通过线性规划的方法对其进行解决.

### 对偶求解

经过ReLU松弛之后, 我们最终的优化问题为:

$$
\forall y^\text{targ} \neq y^\ast, \min_\theta\max_v c^\top v, \\
\text{s.t. } v \in \hat{\mathcal{F}}_{\hat{\mathcal{A}}(x^\ast)}
$$

此时需要计算梯度 $\theta$ 去最小化内部max问题, 即求得 $v^\ast$: $\nabla_\theta \max_v c^\top v = \nabla c^\top  v^\ast$.

根据对偶问题的性质, 我们将内部问题转化为对应的对偶问题, 具体计算步骤可见论文[^1]附录A.2: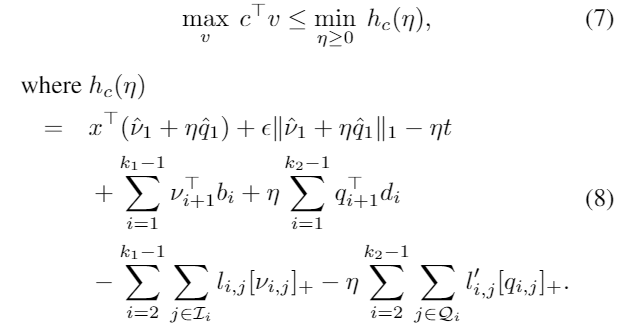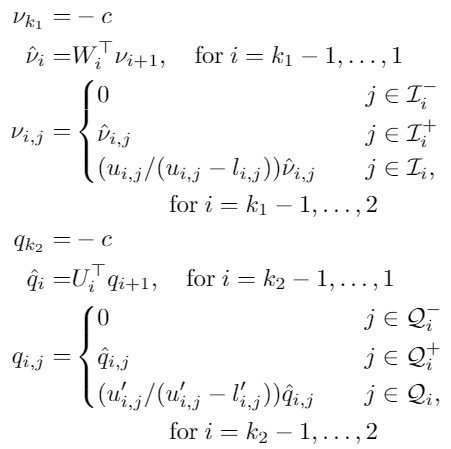
![](/usr/uploads/2022/04/1850269550.png)
![](/usr/uploads/2022/04/370750889.png)

通过转化为对偶问题, 我们将求原问题的 $v^\ast$ 转化为了求得对偶问题的 $\eta$ ($\eta$ 为对偶问题引入的对偶变量), 我们需要求得对偶问题 $h_c(\eta)$ 的极小值. 通过对 $h_c(\eta)$ 求导:

$$
\nabla_\eta h_c(\eta) = \epsilon \gamma(\eta) - t + C, \\
\gamma(\eta) = \sum^n_{j=1}sgn(\hat{v}_{1,j} + \eta\hat{q}_{1,j})
$$

根据对 $hat{q}_{1,j}$ 的分类讨论, 可以得到 $\gamma(\eta)$ 的性质: 有界非递减的阶跃函数, 跳跃点为 $\eta_j = -\hat{v}_{1,j} / \hat{q}_{1,j}$.

由于 $h_c(\eta)$ 是仅有关于对偶变量 $\eta$ 的函数, 因此 $h_c(\eta)$ 与 $\gamma(\eta)$ 有相同的性质.

此时, $h_c(\eta)$ 的定义域为 $[0, \infty]$, 令 $\eta_l=0, \eta_r=\max_j(-\hat{v}_{1,j} / \hat{q}_{1,j})$, 能够得到该梯度的值域:

$$
\nabla_\eta h_c(\eta) \in [\nabla_\eta h_c(\eta)|_{\eta = \eta_l},\nabla_\eta h_c(\eta)|_{\eta = \eta_r}] \equiv [l,r]
$$

对上述值域进行分析, 当:

- $l \leq r \leq 0$ 时, $\eta \to \infty$, $h_c(\eta) \to \infty$. 此时对偶问题无界, 即原问题无界, 不存在空间 $\mathcal{F}_\mathcal{A}(x^\ast)$, 此时需要手动减少 $t$ 以扩大对抗空间.
- $l \leq 0 \leq r$ 时, $\eta$ 存在一个正解, 此时对抗空间的约束是足够紧(tight)的.
- $0 \leq l \leq r$ 时, 存在解 $\eta=0$, 此时模型训练与模型 $g$ 无关, 表示此时对抗空间的约束过于松弛, 应当适当的增加 $t$ 以缩减对抗空间.

通过找到一个合理的 $\eta$, 并以此反向得到 $t$, 以此为内部问题的解, 进而训练外部问题 $\theta$.

## Experiments

实验使用Cross-Entropy作为模型的损失函数.

1. 首先, 独立的随机化两个模型 $f$, $g$
2. 当模型规模较小时, 对于每个epoch

- 先将 $f$ 作为训练模型 而 $g$ 作为引用模型
- 再将 $g$ 作为训练模型 而 $f$ 作为引用模型

3. 当模型规模较大时, 平行训练两个模型 $f$ 和 $g$.

实验使用MNSIT和CIFAR-10作为实验数据, 模型具体参数如下图: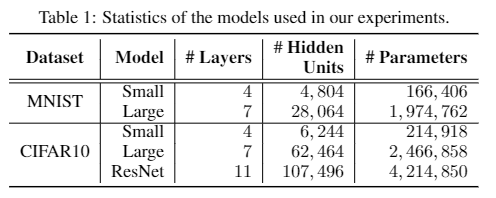
![](/usr/uploads/2022/04/181681178.png)

每个模型和数据集分别跑100个epoch, 其中MNIST使用Adam Optimizer, CIFAR10则使用SGD Optimizer

## Evaluation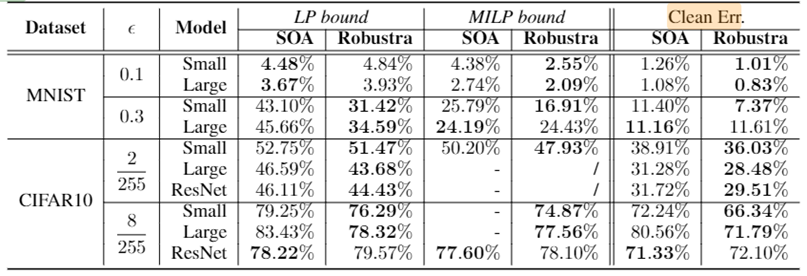

![](/usr/uploads/2022/04/1468656282.png)

> SOTA模型来源: Provable Defenses against Adversarial Examples via the Convex Outer Adversarial Polytope[^1]

可以发现, 本文的方法Robustra在多数数据集下性能都要略优于SOTA模型, 且对于净错误率要远优于SOTA模型.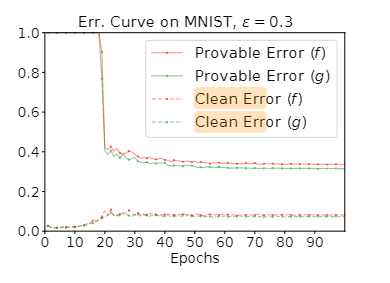

![](/usr/uploads/2022/04/1096357060.png)

根据训练曲线可以看到, 在前20个epoch上, 结果表明除非在该扰动水平上进行训练, 否则该模型对较大的扰动不具有鲁棒性. 除此之外, 在前20个Epoch, 净误差增加, 而可证明鲁棒误差边界减少; 随后, 两者都随着训练地进行而减小.

## Conclusion

- 通过激活函数Relu进行松弛, 并利用了参考模型的对抗空间来作为可行域来解决攻击和防御的min-max问题.
- 通过线性逼近攻击的最佳策略, 同时利用参考模型引入松弛变量的单调性, 来解决对偶问题.
- 相较于目前的SOTA模型, 通过在MNIST和CIFAR 10的实验表明, 该方法生成的DNN具有明显更好的可证明对抗性错误界限

[^1]: Provable Defenses against Adversarial Examples via the Convex Outer Adversarial Polytope
[^2]: Robustra: Training Provable Robust Neural Networks over Reference Adversarial Space

最后修改：2022 年 04 月 05 日

如果觉得我的文章对你有用，请随意赞赏

发表评论取消回复

评论 *

私密评论

名称 *

🎲

邮箱

地址

陈埯猝
陈埯猝:文章真不错http://wap.jst-gpmx.cn...
CrystMiku
最近还用Azure吗，我hk的服务器速度好慢
h_daniel
墙啊大佬，AFO蒟蒻顶礼膜拜orz%%%

Robustra: Training Provable Robust Neural Networks over Reference Adversarial Space

ShaneG_Miku • 2022 年 04 月 05 日

## Abstract

## Introduction

![Adversarial Example of Vision-based DNN](/usr/uploads/2022/04/3663001837.png)

因此, 对于上述的例子, 可以定义: 对于输入样本 $x$ 范式球内的所有 $x'$, 若模型对这两者都能输出相同的标签, 则 Vision-based DNN 是具有鲁棒的:

$$
\forall x':\Vert x-x'\Vert_p \leq \delta \to f(x)=f(x')
$$

## Method

### 问题定义

首先定义一个基于ReLU激活函数的神经网络 $f$, $g$:

$$
\begin{cases}
z_0 = x \in \mathbb{R}^n \\
z_i=\text{ReLU}(W_i z_{i-1} + b_i), 1 \leq i \leq k_1 \\
f(x) = z_{k_1} \in \mathbb{R}^m
\end{cases}
$$

$$
\begin{cases}
w_0 = x \in \mathbb{R}^n \\
w_i=\text{ReLU}(U_i w_{i-1} + d_i), 1 \leq i \leq k_2 \\
g(x) = w_{k_2} \in \mathbb{R}^m
\end{cases}
$$

其中, $f$ 为等待训练的模型, $g$ 引用模型. $\theta$ 为模型 $f$ 中需要训练的参数

给定一个样本: $x^\ast$; 样本标签: $y^\ast$; 目标标签: $y^\text{targ}, y^\text{targ} \neq y^\ast$, 我们可以得到模型 $g$ 在 $l_\infty$ 范数约束下的对抗样本空间:

$$
\mathcal{A}_\epsilon(x^\ast) = \Big\{x:
\big(\Vert x-x^\ast \Vert_\infty \leq \epsilon \big) 
\land 
\Big( \big(g(x)\big)_{y^\text{targ}} - \big(g(x)\big)_{y^\ast} \geq t \Big)
\Big\}
$$

对于上式, 其中 $t$ 为对抗性样例和决策边界之间的距离:

我们的目标是希望从 $g$ 的对抗空间 $\mathcal{A}_\epsilon(x^\ast)$ 的样本训练模型 $f$ , 使模型 $f$ 能够抵御引用模型 $g$ 的对抗样例, 即:

$$
\forall y^\text{targ}, \min_\theta \Big( \max_x \big( f_\theta(x) \big)_{y^\text{targ}} - \big( f_\theta(x) \big)_{y^\ast} \Big), \\
\text{s.t. } x \in \mathcal{A}_\epsilon(x^\ast)
$$

令 $c=e_{y^\text{targ}} - e_{y^\ast}$, $\mathcal{F}_\mathcal{A}(x^\ast)=\{ f_\theta(x): x \in \mathcal{A}_\epsilon(x^\ast)\}$, 上式可以等价改写为:

$$
\forall y^\text{targ}, \min_\theta \max_v c^\top v, \\
\text{s.t. } v \in \mathcal{F}_\mathcal{A}(x^\ast)
$$

接下来, 训练模型 $f$ 的主要问题就是如何求解上式这个优化问题.

### ReLU松弛

![ReLU Relaxation](/usr/uploads/2022/04/1348255019.png)

文章将ReLU函数 $y=\max\{x, 0\}$ , 如上图, 通过松弛:

$$
\begin{cases}
o=0, &l\leq u \leq 0 \\
o=i, &0 \leq l \leq u \\
(u-l) o \leq u(i-l) \land o \geq 0. &i\leq i
\end{cases}
$$

![](/usr/uploads/2022/04/3940231651.png)

根据上图可以发现, 原非凸的问题经过松弛后, 变成了一个凸问题, 此时, 我们可以通过线性规划的方法对其进行解决.

### 对偶求解

经过ReLU松弛之后, 我们最终的优化问题为:

$$
\forall y^\text{targ} \neq y^\ast, \min_\theta\max_v c^\top v, \\
\text{s.t. } v \in \hat{\mathcal{F}}_{\hat{\mathcal{A}}(x^\ast)}
$$

此时需要计算梯度 $\theta$ 去最小化内部max问题, 即求得 $v^\ast$: $\nabla_\theta \max_v c^\top v = \nabla c^\top  v^\ast$.

$$
\nabla_\eta h_c(\eta) = \epsilon \gamma(\eta) - t + C, \\
\gamma(\eta) = \sum^n_{j=1}sgn(\hat{v}_{1,j} + \eta\hat{q}_{1,j})
$$

根据对 $hat{q}_{1,j}$ 的分类讨论, 可以得到 $\gamma(\eta)$ 的性质: 有界非递减的阶跃函数, 跳跃点为 $\eta_j = -\hat{v}_{1,j} / \hat{q}_{1,j}$.

由于 $h_c(\eta)$ 是仅有关于对偶变量 $\eta$ 的函数, 因此 $h_c(\eta)$ 与 $\gamma(\eta)$ 有相同的性质.

此时, $h_c(\eta)$ 的定义域为 $[0, \infty]$, 令 $\eta_l=0, \eta_r=\max_j(-\hat{v}_{1,j} / \hat{q}_{1,j})$, 能够得到该梯度的值域:

$$
\nabla_\eta h_c(\eta) \in [\nabla_\eta h_c(\eta)|_{\eta = \eta_l},\nabla_\eta h_c(\eta)|_{\eta = \eta_r}] \equiv [l,r]
$$

对上述值域进行分析, 当:

通过找到一个合理的 $\eta$, 并以此反向得到 $t$, 以此为内部问题的解, 进而训练外部问题 $\theta$.

## Experiments

实验使用Cross-Entropy作为模型的损失函数.

1. 首先, 独立的随机化两个模型 $f$, $g$
2. 当模型规模较小时, 对于每个epoch

- 先将 $f$ 作为训练模型 而 $g$ 作为引用模型
- 再将 $g$ 作为训练模型 而 $f$ 作为引用模型

3. 当模型规模较大时, 平行训练两个模型 $f$ 和 $g$.

实验使用MNSIT和CIFAR-10作为实验数据, 模型具体参数如下图:
![](/usr/uploads/2022/04/181681178.png)

每个模型和数据集分别跑100个epoch, 其中MNIST使用Adam Optimizer, CIFAR10则使用SGD Optimizer

## Evaluation

![](/usr/uploads/2022/04/1468656282.png)

> SOTA模型来源: Provable Defenses against Adversarial Examples via the Convex Outer Adversarial Polytope[^1]

可以发现, 本文的方法Robustra在多数数据集下性能都要略优于SOTA模型, 且对于净错误率要远优于SOTA模型.

![](/usr/uploads/2022/04/1096357060.png)

## Conclusion

[^1]: Provable Defenses against Adversarial Examples via the Convex Outer Adversarial Polytope
[^2]: Robustra: Training Provable Robust Neural Networks over Reference Adversarial Space

Robustra: Training Provable Robust Neural Networks over Reference Adversarial Space

发表评论取消回复

此内容被密码保护

2022.4.1 - 4.10

2019 新生赛题解

Casbin - Golang中权限控制模型定义和使用

Happy New Year - 2021!!!

Install Arch Linux in WSL2

2022.4.1 - 4.10

论文研读: 可信机器学习的公平性综述

此内容被密码保护

Chapter 8 数据库概论

Robustra: Training Provable Robust Neural Networks over Reference Adversarial Space

发表评论 取消回复

Robustra: Training Provable Robust Neural Networks over Reference Adversarial Space

发表评论取消回复